《2025年全品学练考九年级数学上册苏科版江苏专版》

1. 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

答案： 两个圆心角、两条弧、两条弦

2. 一般地,$n^{\circ }$的圆心角对着$n^{\circ }$的弧,$n^{\circ }的弧对着n^{\circ }$的圆心角.

答案： 圆心角 圆心角

3. 圆心角的度数与它所对的弧的度数相等.

答案： 它所对的弧的度数

1. 如图 14 - 1,在两个同心圆中,$\overset{\frown }{AB}的度数为60^{\circ }$,则$\overset{\frown }{CD}$的度数为$60^{\circ}$.

答案： $60^{\circ}$

2. 如图 14 - 2,在$\odot O$中,$\overset{\frown }{AC}= \overset{\frown }{BD}$,$∠1 = 35^{\circ }$,则$∠2$的度数是$35^{\circ}$.

答案： $35^{\circ}$

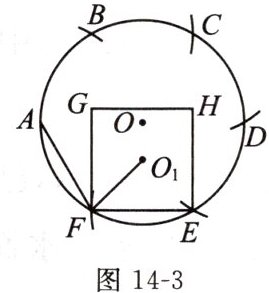
3. 如图 14 - 3,以$\odot O$的半径为半径,自$\odot O$上的点 A 起,在圆上依次画弧截取点 B,C,D,E,F.正方形 EFGH 的中心为点$O_{1}$,连接 FA,$FO_{1}$,则$∠AFO_{1}= $75$^{\circ }$.

答案： 75

4. 如图 14 - 4,在$\odot O$中,弦 AB,CD 相交于点 E,$AD = BC$.
(1)比较$\overset{\frown }{AB}与\overset{\frown }{CD}$的长度,并证明你的结论;
(2)求证:$AE = CE$.

答案： 1. （1）
解：$\overset{\frown }{AB}=\overset{\frown }{CD}$。
证明：因为$AD = BC$，根据在同圆或等圆中，相等的弦所对的弧相等，所以$\overset{\frown }{AD}=\overset{\frown }{BC}$。
又因为$\overset{\frown }{AB}=\overset{\frown }{AD}+\overset{\frown }{DB}$，$\overset{\frown }{CD}=\overset{\frown }{BC}+\overset{\frown }{DB}$，所以$\overset{\frown }{AB}=\overset{\frown }{CD}$。
2. （2）
证明：由（1）知$\overset{\frown }{AB}=\overset{\frown }{CD}$，所以$\angle ADE=\angle CBE$（在同圆或等圆中，等弧所对的圆周角相等）。
在$\triangle ADE$和$\triangle CBE$中，$\left\{\begin{array}{l}\angle AED=\angle CEB\\\angle ADE=\angle CBE\\AD = BC\end{array}\right.$。
根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等），可得$\triangle ADE\cong\triangle CBE$。
所以$AE = CE$（全等三角形的对应边相等）。