一般地,
若n个数$x_{1},x_{2},...,x_{n}$的权分别是$w_{1},w_{2},...,w_{n}$,则$\overline {x}=\frac {x_{1}w_{1}+x_{2}w_{2}+... +x_{n}w_{n}}{w_{1}+w_{2}+... +w_{n}}$
叫做这n个数的加权平均数.
答案:
若n个数$x_{1},x_{2},...,x_{n}$的权分别是$w_{1},w_{2},...,w_{n}$,则$\overline {x}=\frac {x_{1}w_{1}+x_{2}w_{2}+... +x_{n}w_{n}}{w_{1}+w_{2}+... +w_{n}}$
1. 某公司在对员工进行招聘时,主要对员工的专业知识、应变能力和工作能力三方面进行考核,并将这三项成绩分别按30%、20%和50%的比例计算总成绩.小王的各项成绩(单位:分)如下表,则小王的考核总成绩为 (

A. 84分
B. 85分
C. 87分
D. 89分
D
)
A. 84分
B. 85分
C. 87分
D. 89分
答案:
D
2. 为了准确掌握一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,长度x(单位:mm)的数据分布如下表,这些棉花纤维的平均长度是
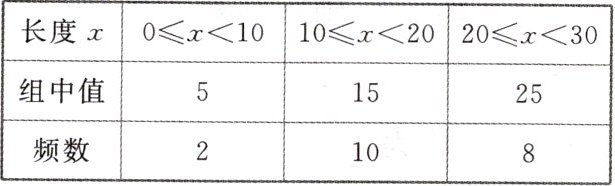
18
mm.
答案:
18
3. 小明在参加岗位应聘时,专业知识、工作经验、仪表形象三项的得分分别为18分、15分、16分.若这三项的重要性之比为5:3:2,求小明最终的得分.
答案:
解:根据加权平均数公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$(其中$x_{i}$为数据,$f_{i}$为权数)。
已知专业知识、工作经验、仪表形象三项得分分别为$x_{1} = 18$分、$x_{2}=15$分、$x_{3}=16$分,重要性之比(权数)为$f_{1}:f_{2}:f_{3}=5:3:2$,设$f_{1} = 5k$,$f_{2}=3k$,$f_{3}=2k$($k\neq0$)。
则小明最终得分$\overline{x}=\frac{18×5k + 15×3k+16×2k}{5k + 3k+2k}$
$=\frac{90k + 45k+32k}{10k}$
$=\frac{167k}{10k}$
$ = 16.7$(分)
答:小明最终的得分是$16.7$分。
已知专业知识、工作经验、仪表形象三项得分分别为$x_{1} = 18$分、$x_{2}=15$分、$x_{3}=16$分,重要性之比(权数)为$f_{1}:f_{2}:f_{3}=5:3:2$,设$f_{1} = 5k$,$f_{2}=3k$,$f_{3}=2k$($k\neq0$)。
则小明最终得分$\overline{x}=\frac{18×5k + 15×3k+16×2k}{5k + 3k+2k}$
$=\frac{90k + 45k+32k}{10k}$
$=\frac{167k}{10k}$
$ = 16.7$(分)
答:小明最终的得分是$16.7$分。
查看更多完整答案,请扫码查看


