《2025年全优课堂九年级数学下册冀教版河北专版》

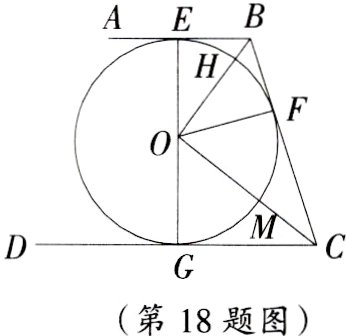
18. 数形结合思想 如图，AB，BC，CD分别与⊙O相切于点E，F，G，且AB//CD，BO = 6，CO = 8.
(1)判断△OBC的形状，并证明你的结论；
(2)求BC的长；
(3)求⊙O的半径OF的长.
　　　　　　　　　　

答案： 解：
(1)△OBC是直角三角形.
证明：
∵AB，BC，CD分别与⊙O相切于点E，F，G，
∴∠OBE = ∠OBF = $\frac{1}{2}$∠EBF，
∠OCG = ∠OCF = $\frac{1}{2}$∠GCF，
∵AB//CD，
∴∠EBF + ∠GCF = 180°，
∴∠OBF + ∠OCF = 90°，
∴∠BOC = 90°，
∴△OBC是直角三角形；
(2)
∵在Rt△BOC中，BO = 6，CO = 8，
∴BC = $\sqrt{BO^{2}+CO^{2}}$ = 10；
(3)
∵BC与⊙O相切于点F，
∴OF⊥BC，
∴$\frac{1}{2}$OF·BC = $\frac{1}{2}$CO·BO，
∴OF = $\frac{BO·CO}{BC}$ = $\frac{6×8}{10}$ = 4.8.

19. 综合实践 应用意识 问题提出：(1)如图1，已知点C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连接AC，EC.若AB = 4，DE = 2，BD = 12，则AC + CE的最小值为 ________；
问题解决：(2)如图2，某公园规划修建一块形如四边形ABCD的牡丹园，其中AD//BC，∠A = 90°，∠C = 60°，AD = 300 m，BC = CD，在△BCD的内心O处修建一个圆形喷水池，公园的入口E是AD的中点，BE是一条观赏小道，其余部分种植牡丹，现需要在AB边上取点F，BE边上取点M，修建道路EF，FM，OM.为了节省成本，需要使修建的道路最短，即EF + FM + OM的值最小，是否存在这样的点F，M，使得EF + FM + OM的值最小？若存在，请求出其最小值；若不存在，请说明理由.
　　　　　　　　　　　　　

答案：
解：
(1)6$\sqrt{5}$ 提示：如图1，连接AE，过点E作EF⊥AB交AB的延长线于点F，
∵∠D = ∠EFA = ∠FBD = 90°，
∴四边形EFBD是矩形，
∴EF = BD = 12，BF = DE = 2，
∴AF = 6，
∴AE = $\sqrt{AF^{2}+EF^{2}}$ = $\sqrt{6^{2}+12^{2}}$ = 6$\sqrt{5}$，
∵AC + CE ≥ AE，
∴AC + CE的最小值为6$\sqrt{5}$；

(2)存在.如图2，作点E关于AB的对称点E'，连接OE'，则EF + FM + OM = E'F + FM + OM ≥ OE'，
连接DO并延长交BC于点H，
∵∠C = 60°，BC = CD，
∴△BCD是等边三角形，
∴∠DBC = 60°，
∵O是△BCD的内心，
∴DH平分∠BDC，BO平分∠CBD，
∴DH⊥BC，∠OBC = $\frac{1}{2}$∠DBC = 30°，
∴2OH = OB，
∵AD//BC，∠BAD = 90°，
∴易知四边形ABHD是矩形，
∴BH = AD = 300 m，
∵OB² = OH² + BH²，
∴OB = OD = 200$\sqrt{3}$ m，
∵AE' = AE = $\frac{1}{2}$AD = 150 m，
∴DE' = 450 m，
∴OE' = $\sqrt{DE'^{2}+OD^{2}}$ = $\sqrt{450^{2}+(200$\sqrt{3}$)^{2}}$ = 50$\sqrt{129}$ (m)，
∴EF + FM + OM的最小值为50$\sqrt{129}$ m.

　　　　　　　　　　　　

答案： 解：
(1)
∵5² + 12² = 13²，
∴这个三角形是直角三角形.
∴这个三角形的面积为$\frac{1}{2}$×5×12 = 30.
设这个三角形内切圆的半径为r，则r = $\frac{30×2}{5 + 12 + 13}$ = 2；
(2)在题图2中连接OA，OB，OC，OD，设四边形的内切圆半径为r，则S四边形ABCD = S△OAB + S△OBC + S△OCD + S△ODA，
又
∵S△OAB = $\frac{1}{2}$AB·r，S△OBC = $\frac{1}{2}$BC·r，S△OCD = $\frac{1}{2}$CD·r，S△ODA = $\frac{1}{2}$DA·r，
∴S四边形ABCD = $\frac{1}{2}$AB·r + $\frac{1}{2}$BC·r + $\frac{1}{2}$CD·r + $\frac{1}{2}$DA·r = $\frac{1}{2}$(AB + BC + CD + DA)·r，
即S四边形ABCD = $\frac{1}{2}$(a + b + c + d)r，
∴r = $\frac{2S_{四边形ABCD}}{a + b + c + d}$；
(3)r = $\frac{2S}{a_{1}+a_{2}+\cdots +a_{n}}$ (r是n边形的内切圆半径).