5.如图,在平面直角坐标系中,点P在第一象限内,⊙P与x轴相切于点C,与y轴相交于点A(0,8),B(0,2).连结AC,BC.
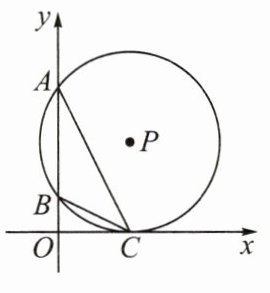
(1)求点P的坐标;
(2)求cos∠ACB的值.
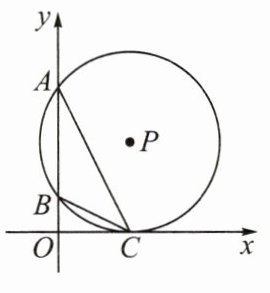
(1)求点P的坐标;
(2)求cos∠ACB的值.
答案:
解:
(1)如图,连结PC,PB,过点P作PD⊥AB于点D,则BD = $\frac{1}{2}$AB,
∵点A(0,8),B(0,2),
∴BD = $\frac{1}{2}$AB = $\frac{1}{2}$(OA - OB) = 3,OD = OB + BD = 5.

∵⊙P与x轴相切于点C,
∴PC = PB,∠PCO = 90°.
∵∠COD = ∠PDO = 90°,
∴四边形OCPD是矩形,
∴PC = OD = 5,
∴PB = 5.
在Rt△PDB中,PD = $\sqrt{PB^{2}-BD^{2}}$ = $\sqrt{5^{2}-3^{2}}$ = 4,
∴点P的坐标为(4,5).
(2)由
(1)知,PA = PB,PD⊥AB,
∴∠DPB = $\frac{1}{2}$∠APB.
∵∠ACB = $\frac{1}{2}$∠APB,
∴∠ACB = ∠DPB.
在Rt△DPB中,cos∠DPB = $\frac{PD}{PB}$ = $\frac{4}{5}$,
∴cos∠ACB = $\frac{4}{5}$.
解:
(1)如图,连结PC,PB,过点P作PD⊥AB于点D,则BD = $\frac{1}{2}$AB,
∵点A(0,8),B(0,2),
∴BD = $\frac{1}{2}$AB = $\frac{1}{2}$(OA - OB) = 3,OD = OB + BD = 5.

∵⊙P与x轴相切于点C,
∴PC = PB,∠PCO = 90°.
∵∠COD = ∠PDO = 90°,
∴四边形OCPD是矩形,
∴PC = OD = 5,
∴PB = 5.
在Rt△PDB中,PD = $\sqrt{PB^{2}-BD^{2}}$ = $\sqrt{5^{2}-3^{2}}$ = 4,
∴点P的坐标为(4,5).
(2)由
(1)知,PA = PB,PD⊥AB,
∴∠DPB = $\frac{1}{2}$∠APB.
∵∠ACB = $\frac{1}{2}$∠APB,
∴∠ACB = ∠DPB.
在Rt△DPB中,cos∠DPB = $\frac{PD}{PB}$ = $\frac{4}{5}$,
∴cos∠ACB = $\frac{4}{5}$.
典例解析
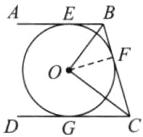
例1 如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB//CD,OB = 6 cm,OC = 8 cm. 求:
(1)∠BOC的度数;
(2)BE + CG的长;
(3)⊙O的半径.

分析:(1)连结OF. 根据切线的性质得到BO平分∠EBF,CO平分∠GCF,OF⊥BC,再根据平行线的性质求解;
(2)由勾股定理可求得BC的长,进而由切线长定理可得到BE + CG的长;
(3)由三角形的面积公式即可求得OF的长.
例1 如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB//CD,OB = 6 cm,OC = 8 cm. 求:
(1)∠BOC的度数;
(2)BE + CG的长;
(3)⊙O的半径.

分析:(1)连结OF. 根据切线的性质得到BO平分∠EBF,CO平分∠GCF,OF⊥BC,再根据平行线的性质求解;
(2)由勾股定理可求得BC的长,进而由切线长定理可得到BE + CG的长;
(3)由三角形的面积公式即可求得OF的长.
答案:
解:
(1)如图,连结OF.根据切线长定理得BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.
∵AB//CD,
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°.
(2)由
(1)知,∠BOC=90°.
∵OB = 6 cm,OC = 8 cm,
∴由勾股定理得BC = $\sqrt{OB^{2}+OC^{2}}$ = 10(cm),
∴BE + CG = BC = 10(cm).
(3)
∵OF⊥BC,
∴OF = $\frac{OB\cdot OC}{BC}$ = 4.8(cm).
解:
(1)如图,连结OF.根据切线长定理得BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.

∵AB//CD,
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°.
(2)由
(1)知,∠BOC=90°.
∵OB = 6 cm,OC = 8 cm,
∴由勾股定理得BC = $\sqrt{OB^{2}+OC^{2}}$ = 10(cm),
∴BE + CG = BC = 10(cm).
(3)
∵OF⊥BC,
∴OF = $\frac{OB\cdot OC}{BC}$ = 4.8(cm).
查看更多完整答案,请扫码查看


