《2025年新课程实践与探究丛书九年级数学下册华师大版》

例2　如图,已知直线AB经过⊙O上的点A,且AB = OA,∠OBA = 45°,直线AB是⊙O的切线吗？为什么？

答案： 解：直线AB是⊙O的切线.
∵AB = OA，且∠OBA = 45°，
∴∠AOB = 45°，∠OAB = 90°.
根据经过半径的外端且垂直于这条半径的直线是圆的切线，
∴直线AB是⊙O的切线.

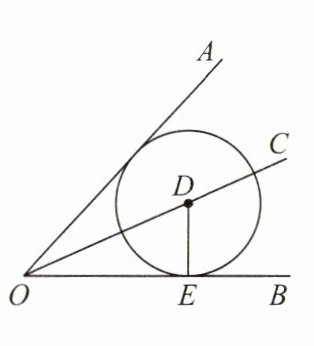
1.如图,D是∠AOB的平分线OC上任意一点,过点D作DE⊥OB于点E,以点D 为圆心、DE的长为半径作⊙D.
(1)判断⊙D与OA的位置关系,并证明你的结论;
(2)通过上述证明,你还能得出哪些等量关系？

答案： 解：
(1)⊙D与OA的位置关系是相切，证明略.
(2)∠DOA = ∠DOE.