《2025年新课程实践与探究丛书九年级数学下册华师大版》

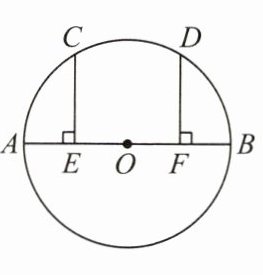
2. 如图，AB为⊙O的直径，点C，D在⊙O上，CE⊥AB于点E，DF⊥AB于点F，且$\overset{\frown}{AC}$与$\overset{\frown}{BD}$相等，则AE与BF是否相等？为什么？

答案：
解：相等. 理由：如图，连结 $OC$，$OD$。

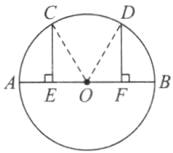
$\because\overset{\frown}{AC}$ 与 $\overset{\frown}{BD}$ 相等，$\therefore\angle COE = \angle DOF$。
又 $\because CE\perp AB$，$DF\perp AB$，$OC = OD$，
$\therefore\triangle OCE\cong\triangle ODF$，$\therefore OE = OF$，$\therefore AE = BF$。

3. 如图，在⊙O中，弦AB = CD，连结AC，BD，求证：AC = BD.

答案： 证明：$\because AB = CD$，$\therefore\overset{\frown}{AB}=\overset{\frown}{CD}$。
$\because\overset{\frown}{BC}=\overset{\frown}{BC}$，$\therefore\overset{\frown}{AC}=\overset{\frown}{BD}$，$\therefore AC = BD$。

4. 如图，在⊙O中，AB，CD为⊙O的直径，E为$\overset{\frown}{BC}$上一点，AC = CE，求证：BD = CE.

答案： 证明：$\because AC = CE$，$\therefore\overset{\frown}{AC}=\overset{\frown}{CE}$。
$\because\angle AOC = \angle BOD$，$\therefore\overset{\frown}{AC}=\overset{\frown}{BD}$，$\therefore BD = CE$。

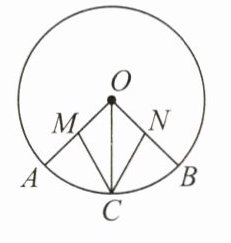
5. 如图，在⊙O中，OA，OB，OC是⊙O的三条半径，C是$\overset{\frown}{AB}$的中点，M，N分别是OA，OB的中点，连结MC，NC. 求证：MC = NC.

答案： 证明：$\because\overset{\frown}{AC}$ 和 $\overset{\frown}{BC}$ 相等，$\therefore\angle AOC = \angle BOC$。
又 $\because OA = OB$，$M$，$N$ 分别是 $OA$，$OB$ 的中点，
$\therefore OM = ON$。
在 $\triangle MOC$ 和 $\triangle NOC$ 中，
$\begin{cases}OM = ON,\\\angle AOC = \angle BOC,\\OC = OC,\end{cases}\therefore\triangle MOC\cong\triangle NOC$，$\therefore MC = NC$。