典例解析
例2 如图,AB是⊙O的弦,C是AB的中点,连结OC并延长交⊙O于点D. 若CD = 2,AB = 8,则⊙O的直径是( )
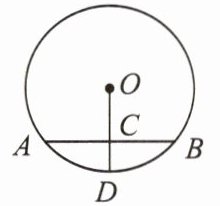
A.2$\sqrt{5}$ B.4$\sqrt{5}$ C.5 D.10
分析:连结OA,根据垂径定理求出AC的长,再由勾股定理可得出OA的长.
例2 如图,AB是⊙O的弦,C是AB的中点,连结OC并延长交⊙O于点D. 若CD = 2,AB = 8,则⊙O的直径是( )

A.2$\sqrt{5}$ B.4$\sqrt{5}$ C.5 D.10
分析:连结OA,根据垂径定理求出AC的长,再由勾股定理可得出OA的长.
答案:
D
变式训练
3. 如图,在⊙O中,AB是直径,弦CD⊥AB于点E. 若AB = 10 cm,CD = 8 cm,则BE的长为( )
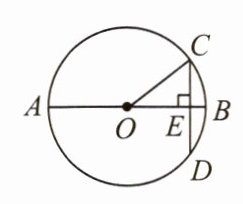
A.5 cm
B.3 cm
C.2 cm
D.1.5 cm
3. 如图,在⊙O中,AB是直径,弦CD⊥AB于点E. 若AB = 10 cm,CD = 8 cm,则BE的长为( )

A.5 cm
B.3 cm
C.2 cm
D.1.5 cm
答案:
C
4. 如图,在⊙O中,半径OC的长为r cm,弦AB与OC垂直,将⊙O沿AB折叠,$\overset{\frown}{AB}$恰好经过OC的中点D. 若弦AB的长为4$\sqrt{15}$ cm,则r = ________cm.
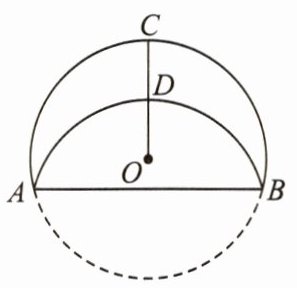

答案:
8
典例解析
例3 如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交$\overset{\frown}{BC}$于点D,已知BC = 8,ED = 2.
(1)求⊙O的半径;
(2)求AC的长.

例3 如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交$\overset{\frown}{BC}$于点D,已知BC = 8,ED = 2.
(1)求⊙O的半径;
(2)求AC的长.

答案:
略
变式训练
5. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E. 若OE = 3,OB = 5,则CD的长为( )
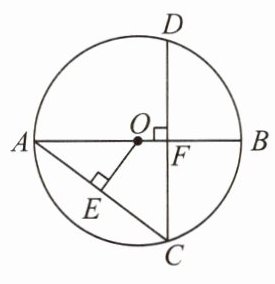
A.9.6
B.4$\sqrt{5}$
C.5$\sqrt{3}$
D.19
5. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E. 若OE = 3,OB = 5,则CD的长为( )

A.9.6
B.4$\sqrt{5}$
C.5$\sqrt{3}$
D.19
答案:
A
典例解析
例4 如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD//AB,AB = 26 m,OE⊥CD于点E. 水位正常时测得OE : CD = 5 : 24.
(1)求CD的长;
(2)现汛期来临,水面以4 m/h的速度上升,则经过多长时间桥洞会刚好被灌满?
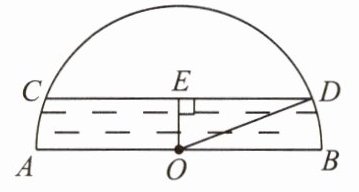
分析:(1)在Rt△EOD中,利用勾股定理求得ED的长,2ED即为弦CD的长;
(2)延长OE交⊙O于点F,求得EF的长,然后求经过的时间.
例4 如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD//AB,AB = 26 m,OE⊥CD于点E. 水位正常时测得OE : CD = 5 : 24.
(1)求CD的长;
(2)现汛期来临,水面以4 m/h的速度上升,则经过多长时间桥洞会刚好被灌满?

分析:(1)在Rt△EOD中,利用勾股定理求得ED的长,2ED即为弦CD的长;
(2)延长OE交⊙O于点F,求得EF的长,然后求经过的时间.
答案:
解:
(1)
∵ 直径$AB = 26\ m$,
$\therefore OD=\frac{1}{2}AB=\frac{1}{2}\times26 = 13(m)$。
$\because OE\perp CD$,$\therefore DE=\frac{1}{2}CD$。
$\because OE:CD = 5:24$,$\therefore OE:ED = 5:12$。
设$OE = 5x$,$ED = 12x$,$\therefore$ 在$Rt\triangle ODE$中,$(5x)^{2}+(12x)^{2}=13^{2}$,解得$x = 1$,$\therefore CD = 2DE = 2\times12 = 24(m)$。
(2)由
(1)得$OE = 5\ m$,延长$OE$交$\odot O$于点$F$,
$\therefore EF = OF - OE = 13 - 5 = 8(m)$,
$\therefore\frac{8}{4}=2(h)$,即经过$2\ h$桥洞会刚好被灌满。
(1)
∵ 直径$AB = 26\ m$,
$\therefore OD=\frac{1}{2}AB=\frac{1}{2}\times26 = 13(m)$。
$\because OE\perp CD$,$\therefore DE=\frac{1}{2}CD$。
$\because OE:CD = 5:24$,$\therefore OE:ED = 5:12$。
设$OE = 5x$,$ED = 12x$,$\therefore$ 在$Rt\triangle ODE$中,$(5x)^{2}+(12x)^{2}=13^{2}$,解得$x = 1$,$\therefore CD = 2DE = 2\times12 = 24(m)$。
(2)由
(1)得$OE = 5\ m$,延长$OE$交$\odot O$于点$F$,
$\therefore EF = OF - OE = 13 - 5 = 8(m)$,
$\therefore\frac{8}{4}=2(h)$,即经过$2\ h$桥洞会刚好被灌满。
查看更多完整答案,请扫码查看


