典例解析
例1 如图,已知AB是⊙O的直径,则下列说法正确的有( )
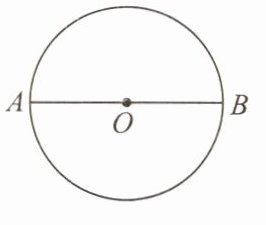
①⊙O是轴对称图形;
②线段AB是⊙O的对称轴;
③直线AB是⊙O的对称轴;
④⊙O绕圆心旋转90°之后能与自身重合.
A. 1个 B. 2个
C. 3个 D. 4个
例1 如图,已知AB是⊙O的直径,则下列说法正确的有( )

①⊙O是轴对称图形;
②线段AB是⊙O的对称轴;
③直线AB是⊙O的对称轴;
④⊙O绕圆心旋转90°之后能与自身重合.
A. 1个 B. 2个
C. 3个 D. 4个
答案:
C
变式训练
1. 如图所示是两个同心圆,其中两条直径互相垂直,大圆的半径是2,则阴影部分的面积之和为______.

1. 如图所示是两个同心圆,其中两条直径互相垂直,大圆的半径是2,则阴影部分的面积之和为______.

答案:
$2\pi$
典例解析
例2 如图,AB是⊙O的直径,$\overset{\frown}{BC}=\overset{\frown}{CD}=\overset{\frown}{DE}$,∠COD = 38°,则∠AEO的度数是( )
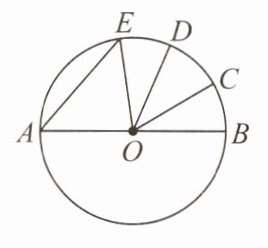
A. 52° B. 57°
C. 66° D. 78°
分析:可求得∠BOC = ∠EOD = ∠COD = 38°,继而可求得∠AOE的度数,然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数.
例2 如图,AB是⊙O的直径,$\overset{\frown}{BC}=\overset{\frown}{CD}=\overset{\frown}{DE}$,∠COD = 38°,则∠AEO的度数是( )

A. 52° B. 57°
C. 66° D. 78°
分析:可求得∠BOC = ∠EOD = ∠COD = 38°,继而可求得∠AOE的度数,然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数.
答案:
B
查看更多完整答案,请扫码查看


