《2025年新课程实践与探究丛书九年级数学下册华师大版》

变式训练
4.某商店销售一种进价为50元/件的商品，售价为60元/件，每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.设每件商品的售价上涨x元(x为正整数),每星期销售该商品的利润为y元,则y关于x的函数表达式为(　　　)
A.y=−10x²+100x+2000
B.y=10x²+100x+2000
C.y=−10x²+200x
D.y=−10x²−100x+2000

答案： A

5.下列关系中，是二次函数关系的是(　　　)
A.当距离s一定时,汽车行驶的时间t与速度v之间的关系
B.在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系
C.圆的面积S与圆的半径r之间的关系
D.正方形的周长C与边长a之间的关系

答案： C

6.某公司决定对原价为33元的某产品分两次进行降价,若设平均每次降价的百分比为x,降价后的价格为y元,则y与x之间的函数关系式为(　　　)
A.y=33×2(1−x)
B.y=33×2(1−x²)
C.y=33×(1−x)²
D.y=33(1−x)

答案： C

7.已知二次函数y=αx²,当x=3时,y=−5;当x=−5时,y的值为________.

答案： $-\frac{125}{9}$

8.如图,小李家用40m长的篱笆围成一
个一边靠墙(墙足够长)的矩形菜园.
　　　　　　　
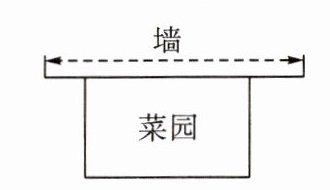
(1)写出这块菜园的面积y(m²)关于垂直于墙的边长x(m)的函数表达式;
(2)直接写出x的取值范围.

答案： 解：
(1)$y = - 2x^{2}+40x$.
(2)$0 ＜ x ＜ 20$.