《2025年新课程实践与探究丛书九年级数学下册华师大版》

典例解析
例1 画出二次函数$y = x^{2}$的图象.
解:列表:
|$x$|$\cdots$|$-3$|$-2$|$-1$|$0$|$1$|$2$|$3$|$\cdots$|
|$y$|$\cdots$| | | | | | | |$\cdots$|
描点,并连线(平滑的曲线).

注意两点:
(1)由于我们只描出了7个点,但自变量取值范围是实数,故我们只画出了实际图象的一部分,即画出了图象在原点附近、自变量在$-3$到$3$这个区间的一部分. 而图象在$x ＞ 3$或$x ＜ - 3$的区间是无限延伸的.
(2)所画的图象是近似的. 像这样的曲线通常叫抛物线. 它有一条对称轴,抛物线与它的对称轴的交点叫抛物线的顶点.
由二次函数$y = x^{2}$的图象可知:
(1)二次函数$y = x^{2}$的图象是一条______，有时也叫抛物线$y = x^{2}$.
(2)在二次函数$y = x^{2}$中,$x^{2}$的系数为______，抛物线$y = x^{2}$的图象开口______(填“向上”或“向下”).
(3)二次函数$y = x^{2}$的图象是______图形,对称轴是______(或直线______).
(4)抛物线与对称轴的交点叫抛物线的______. 抛物线$y = x^{2}$的顶点坐标为$(0,0)$,是图象的______(填“最高”或“最低”)点.

答案： 略

变式训练
1. 在平面直角坐标系中,二次函数$y = \frac{1}{2}x^{2}$的图象如图所示.

(1)根据已知的图象部分画出该函数图象的另一部分;(直接在网格中作图即可)
(2)判断点$(-2,-4)$是否在该函数图象上,并说明理由;
(3)求当$y = 4$时对应的函数图象上的点的坐标.

答案：
解：
(1)如图：

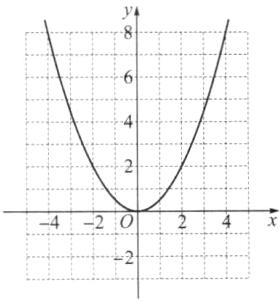
(2)当$x = - 2$时，$y=\frac{1}{2}\times(-2)^{2}=2$，
$\therefore$点$(-2,-4)$不在该函数图象上.
(3)当$y = 4$时，由$4=\frac{1}{2}x^{2}$，得$x=\pm2\sqrt{2}$，
$\therefore$当$y = 4$时，对应的函数图象上的点的坐标为$(2\sqrt{2},4)$和$(-2\sqrt{2},4)$.