变式训练
1. 顶点坐标为$(-6,0)$、开口向下、形状与函数$y = \frac{1}{2}x^{2}$的图象相同的抛物线所对应的函数表达式是__________.
1. 顶点坐标为$(-6,0)$、开口向下、形状与函数$y = \frac{1}{2}x^{2}$的图象相同的抛物线所对应的函数表达式是__________.
答案:
$y = -\frac{1}{2}(x + 6)^{2}$
2. 在平面直角坐标系中,二次函数$y = x^{2}-mx + n$的图象与$y$轴的交点到坐标原点的距离是2,且函数图象的对称轴为直线$x = 1$,求该函数的表达式.
答案:
解:由对称轴为直线$x = 1$,得$-\frac{-m}{2}=1$,解得$m = 2$.
$\because$二次函数$y = x^{2}-mx + n$的图象与$y$轴的交点到坐标原点的距离是 2,则与$y$轴的交点坐标是$(0,2)$或$(0,-2)$,则有以下两种情况:
①当与$y$轴的交点坐标是$(0,2)$时,代入$y = x^{2}-2x + n$,得$n = 2$,则函数的表达式是$y = x^{2}-2x + 2$;
②当与$y$轴的交点坐标是$(0,-2)$时,代入$y = x^{2}-2x + n$,得$n = -2$,则函数的表达式是$y = x^{2}-2x - 2$.
综上所述,函数的表达式为$y = x^{2}-2x + 2$或$y = x^{2}-2x - 2$.
$\because$二次函数$y = x^{2}-mx + n$的图象与$y$轴的交点到坐标原点的距离是 2,则与$y$轴的交点坐标是$(0,2)$或$(0,-2)$,则有以下两种情况:
①当与$y$轴的交点坐标是$(0,2)$时,代入$y = x^{2}-2x + n$,得$n = 2$,则函数的表达式是$y = x^{2}-2x + 2$;
②当与$y$轴的交点坐标是$(0,-2)$时,代入$y = x^{2}-2x + n$,得$n = -2$,则函数的表达式是$y = x^{2}-2x - 2$.
综上所述,函数的表达式为$y = x^{2}-2x + 2$或$y = x^{2}-2x - 2$.
典例解析
例2 在平面直角坐标系中,二次函数的图象过点$(0,1)$,$(2,4)$,$(3,10)$,求该二次函数的表达式.
例2 在平面直角坐标系中,二次函数的图象过点$(0,1)$,$(2,4)$,$(3,10)$,求该二次函数的表达式.
答案:
$y = \frac{3}{2}x^{2}-\frac{3}{2}x + 1$.
变式训练
3. 在平面直角坐标系中,二次函数$y = ax^{2}+bx + c(a\neq0)$的图象过点$A(-1,0)$,$B(2,0)$,$C(0,-2)$,则该二次函数的表达式是__________.
3. 在平面直角坐标系中,二次函数$y = ax^{2}+bx + c(a\neq0)$的图象过点$A(-1,0)$,$B(2,0)$,$C(0,-2)$,则该二次函数的表达式是__________.
答案:
$y = x^{2}-x - 2$
4. 已知二次函数$y = ax^{2}+bx + c(a\neq0)$,函数值$y$与自变量$x$的部分对应值如表:
|$x$|$\cdots$|$-2$|$-1$|$0$|$2$|$\cdots$|
|$y$|$\cdots$|$-3$|$-4$|$-3$|$5$|$\cdots$|
求该二次函数的表达式.
|$x$|$\cdots$|$-2$|$-1$|$0$|$2$|$\cdots$|
|$y$|$\cdots$|$-3$|$-4$|$-3$|$5$|$\cdots$|
求该二次函数的表达式.
答案:
解:将$(0,-3)$代入$y = ax^{2}+bx + c$,得$c = -3$,
$\therefore y = ax^{2}+bx - 3$,
将$(2,5)$和$(-1,-4)$代入$y = ax^{2}+bx - 3$,
得$\begin{cases}4a + 2b - 3 = 5 \\ a - b - 3 = -4 \end{cases}$,解得$\begin{cases} a = 1 \\ b = 2 \end{cases}$,$\therefore y = x^{2}+2x - 3$.
$\therefore y = ax^{2}+bx - 3$,
将$(2,5)$和$(-1,-4)$代入$y = ax^{2}+bx - 3$,
得$\begin{cases}4a + 2b - 3 = 5 \\ a - b - 3 = -4 \end{cases}$,解得$\begin{cases} a = 1 \\ b = 2 \end{cases}$,$\therefore y = x^{2}+2x - 3$.
5. 如图,在平面直角坐标系中,二次函数的图象经过点$A(-1,0)$,$B(5,0)$,$C(0,-2)$.
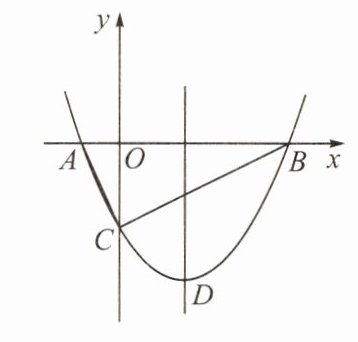
(1)求该二次函数的表达式;
(2)求$\triangle ABC$的面积;
(3)若点$E$在二次函数的图象上,且$\triangle ABE$的面积是$\triangle ABC$面积的一半,求点$E$的坐标.

(1)求该二次函数的表达式;
(2)求$\triangle ABC$的面积;
(3)若点$E$在二次函数的图象上,且$\triangle ABE$的面积是$\triangle ABC$面积的一半,求点$E$的坐标.
答案:
解:
(1)设二次函数的表达式为$y = ax^{2}+bx + c(a\neq0)$,
由题意可知,函数的图象经过点$A(-1,0)$,$B(5,0)$,$C(0,-2)$,将三点的坐标分别代入二次函数的表达式,得
$\begin{cases}a - b + c = 0 \\ 25a + 5b + c = 0 \\ c = -2 \end{cases}$,解得$\begin{cases}a = \frac{2}{5} \\ b = -\frac{8}{5} \\ c = -2 \end{cases}$,
$\therefore$二次函数的表达式为$y = \frac{2}{5}x^{2}-\frac{8}{5}x - 2$.
(2)$\because$点$A(-1,0)$,$B(5,0)$,$C(0,-2)$,
$\therefore AB = 6$,$OC = 2$,$\therefore S_{\triangle ABC}=\frac{1}{2}\times6\times2 = 6$.
(3)设点$E$的纵坐标为$n$,
$\because S_{\triangle ABE}=\frac{1}{2}S_{\triangle ABC}$,$\therefore S_{\triangle ABE}=3$,即$\frac{1}{2}AB\cdot|n| = 3$,
$\because AB = 6$,解得$n = \pm1$,
当$n = 1$时,$\frac{2}{5}x^{2}-\frac{8}{5}x - 2 = 1$,
整理得$2x^{2}-8x - 15 = 0$,
解得$x_{1}=\frac{4+\sqrt{46}}{2}$,$x_{2}=\frac{4-\sqrt{46}}{2}$,
点$E$的坐标为$(\frac{4+\sqrt{46}}{2},1)$或$(\frac{4-\sqrt{46}}{2},1)$;
当$n = -1$时,$\frac{2}{5}x^{2}-\frac{8}{5}x - 2 = -1$,
整理得$2x^{2}-8x - 5 = 0$,解得$x_{1}=\frac{4+\sqrt{26}}{2}$,$x_{2}=\frac{4-\sqrt{26}}{2}$,
点$E$的坐标为$(\frac{4+\sqrt{26}}{2},-1)$或$(\frac{4-\sqrt{26}}{2},-1)$.
综上所述,点$E$的坐标为$(\frac{4+\sqrt{26}}{2},-1)$或$(\frac{4-\sqrt{26}}{2},-1)$或$(\frac{4+\sqrt{46}}{2},1)$或$(\frac{4-\sqrt{46}}{2},1)$.
(1)设二次函数的表达式为$y = ax^{2}+bx + c(a\neq0)$,
由题意可知,函数的图象经过点$A(-1,0)$,$B(5,0)$,$C(0,-2)$,将三点的坐标分别代入二次函数的表达式,得
$\begin{cases}a - b + c = 0 \\ 25a + 5b + c = 0 \\ c = -2 \end{cases}$,解得$\begin{cases}a = \frac{2}{5} \\ b = -\frac{8}{5} \\ c = -2 \end{cases}$,
$\therefore$二次函数的表达式为$y = \frac{2}{5}x^{2}-\frac{8}{5}x - 2$.
(2)$\because$点$A(-1,0)$,$B(5,0)$,$C(0,-2)$,
$\therefore AB = 6$,$OC = 2$,$\therefore S_{\triangle ABC}=\frac{1}{2}\times6\times2 = 6$.
(3)设点$E$的纵坐标为$n$,
$\because S_{\triangle ABE}=\frac{1}{2}S_{\triangle ABC}$,$\therefore S_{\triangle ABE}=3$,即$\frac{1}{2}AB\cdot|n| = 3$,
$\because AB = 6$,解得$n = \pm1$,
当$n = 1$时,$\frac{2}{5}x^{2}-\frac{8}{5}x - 2 = 1$,
整理得$2x^{2}-8x - 15 = 0$,
解得$x_{1}=\frac{4+\sqrt{46}}{2}$,$x_{2}=\frac{4-\sqrt{46}}{2}$,
点$E$的坐标为$(\frac{4+\sqrt{46}}{2},1)$或$(\frac{4-\sqrt{46}}{2},1)$;
当$n = -1$时,$\frac{2}{5}x^{2}-\frac{8}{5}x - 2 = -1$,
整理得$2x^{2}-8x - 5 = 0$,解得$x_{1}=\frac{4+\sqrt{26}}{2}$,$x_{2}=\frac{4-\sqrt{26}}{2}$,
点$E$的坐标为$(\frac{4+\sqrt{26}}{2},-1)$或$(\frac{4-\sqrt{26}}{2},-1)$.
综上所述,点$E$的坐标为$(\frac{4+\sqrt{26}}{2},-1)$或$(\frac{4-\sqrt{26}}{2},-1)$或$(\frac{4+\sqrt{46}}{2},1)$或$(\frac{4-\sqrt{46}}{2},1)$.
查看更多完整答案,请扫码查看


