第159页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
考点一 解决稍复杂的实际问题
例题1 王阿姨以1元2个苹果的价格买进一批苹果,又以2元3个苹果的价格将这些苹果卖出,结果一共赚得20元。王阿姨买进的这批苹果有多少个?
例题1 王阿姨以1元2个苹果的价格买进一批苹果,又以2元3个苹果的价格将这些苹果卖出,结果一共赚得20元。王阿姨买进的这批苹果有多少个?
答案:
思路导引:本题中的条件比较复杂,已知买进苹果的价格为1元2个,卖出苹果的价格为2元3个,可以将买进和卖出苹果的价格转化为3元6个和4元6个,从而可知6个苹果的利润为1元,现在一共赚得20元,再求出这批苹果的总个数。
完全解答:2和3的最小公倍数是6
2×(6÷3) - 1×(6÷2)=1(元)
20÷1×6 = 120(个)
答:王阿姨买进的这批苹果有120个。
点评苑:解决稍复杂的实际问题时,我们可以先分析题中的条件,然后将条件进行转化,从而解决问题。
完全解答:2和3的最小公倍数是6
2×(6÷3) - 1×(6÷2)=1(元)
20÷1×6 = 120(个)
答:王阿姨买进的这批苹果有120个。
点评苑:解决稍复杂的实际问题时,我们可以先分析题中的条件,然后将条件进行转化,从而解决问题。
考点二 用综合法或分析法解决问题
例题2 一个工厂加工一批零件,计划每天加工360个,18天完成,实际每天多加工72个。照这样计算,这个工厂能提前几天完成任务?
例题2 一个工厂加工一批零件,计划每天加工360个,18天完成,实际每天多加工72个。照这样计算,这个工厂能提前几天完成任务?
答案:
思路导引:本题可采用综合法或分析法解答。
综合法:从题中的已知条件入手进行推理,直到解决问题。如图:

分析法:从问题入手进行逆推,寻找解题的条件,直到所需的条件都已知。如图:

完全解答:18 - 360×18÷(360 + 72)=3(天)
答:这个工厂能提前3天完成任务。
点评苑:解决问题时也可以将综合法和分析法结合起来运用。用综合法和分析法这两种方法解题的关键是抓住数量之间的关系来思考。
思路导引:本题可采用综合法或分析法解答。
综合法:从题中的已知条件入手进行推理,直到解决问题。如图:

分析法:从问题入手进行逆推,寻找解题的条件,直到所需的条件都已知。如图:

完全解答:18 - 360×18÷(360 + 72)=3(天)
答:这个工厂能提前3天完成任务。
点评苑:解决问题时也可以将综合法和分析法结合起来运用。用综合法和分析法这两种方法解题的关键是抓住数量之间的关系来思考。
考点三 用列举的策略解决稍复杂的实际问题
例题3 王师傅准备用16米长的篱笆一面靠墙围成一块长方形菜地。如果要使长、宽都是整米数,那么有多少种不同的围法?怎样围面积最大?
例题3 王师傅准备用16米长的篱笆一面靠墙围成一块长方形菜地。如果要使长、宽都是整米数,那么有多少种不同的围法?怎样围面积最大?
答案:
思路导引:根据题意画出如下示意图。因为一面靠墙围,所以篱笆的长 = 墙的邻边长×2 + 墙的对边长。

从墙的邻边长为1米开始考虑,列举出所有的围法。求出面积后,找出其中面积最大的。
完全解答:

答:有7种不同的围法,围成宽4米、长8米的长方形时,面积最大。
点评苑:用列举的策略解决问题的最大优点是不重复,但还要做到不遗漏,需要按照一定的顺序列举。
思路导引:根据题意画出如下示意图。因为一面靠墙围,所以篱笆的长 = 墙的邻边长×2 + 墙的对边长。

从墙的邻边长为1米开始考虑,列举出所有的围法。求出面积后,找出其中面积最大的。
完全解答:

答:有7种不同的围法,围成宽4米、长8米的长方形时,面积最大。
点评苑:用列举的策略解决问题的最大优点是不重复,但还要做到不遗漏,需要按照一定的顺序列举。
考点四 用列表的策略解决问题
例题4 甲仓库有存粮60吨,乙仓库有存粮20吨。每次从甲仓库运4吨粮食到乙仓库,几次后甲、乙两仓库的存粮质量相等?
例题4 甲仓库有存粮60吨,乙仓库有存粮20吨。每次从甲仓库运4吨粮食到乙仓库,几次后甲、乙两仓库的存粮质量相等?
答案:
思路导引:每次从甲仓库运4吨粮食到乙仓库,两仓库的存粮质量会发生相应的变化,可用列表的策略呈现变化情况,直至找出当甲、乙两仓库的存粮质量相等时是第几次运。
完全解答:

答:5次后甲、乙两仓库的存粮质量相等。
点评苑:解决这类在相关联的两个量之间发生变化的问题时,可以用列表的策略。
思路导引:每次从甲仓库运4吨粮食到乙仓库,两仓库的存粮质量会发生相应的变化,可用列表的策略呈现变化情况,直至找出当甲、乙两仓库的存粮质量相等时是第几次运。
完全解答:

答:5次后甲、乙两仓库的存粮质量相等。
点评苑:解决这类在相关联的两个量之间发生变化的问题时,可以用列表的策略。
考点五 用多种策略解决问题
例题5 张叔叔公司组织员工开展团建活动,在浅水湾进行竞走比赛。张叔叔每分钟可竞走100米,如果每走30分钟休息5分钟,那么从上午8时到上午9时30分,张叔叔一共竞走了多少米?
例题5 张叔叔公司组织员工开展团建活动,在浅水湾进行竞走比赛。张叔叔每分钟可竞走100米,如果每走30分钟休息5分钟,那么从上午8时到上午9时30分,张叔叔一共竞走了多少米?
答案:
思路导引:方法一:列表整理题中信息。
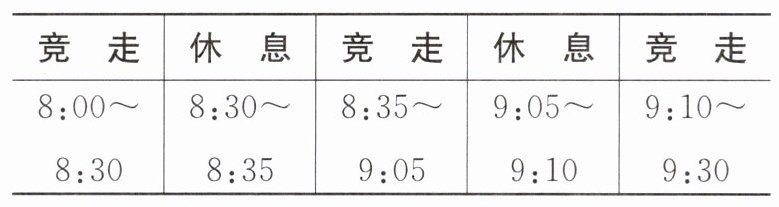
由表可知,从上午8时到上午9时30分,张叔叔休息了2次,一共10分钟。
方法二:画图理解题意。
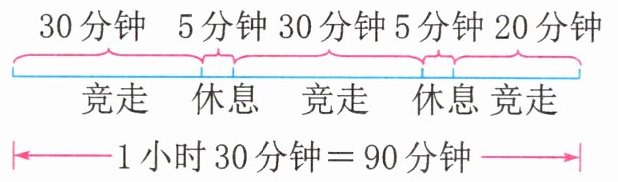
由图可知,90分钟内张叔叔一共休息了10分钟。
方法三:可以把张叔叔每次竞走和休息的时间30 + 5 = 35(分)看作一个周期,看上午8时到上午9时30分里有几个35分,9时30分 - 8时 = 1时30分 = 90分,90÷35 = 2(个)……20(分),余的20分比30分短,所以张叔叔这20分都在竞走,而在2个35分里,张叔叔休息了2个5分,一共休息了2×5 = 10(分)。
所以张叔叔竞走的时间是90-5x2=80(分),再用“速度X时间”求出张叔叔一共竞走的路程。
思路导引:方法一:列表整理题中信息。

由表可知,从上午8时到上午9时30分,张叔叔休息了2次,一共10分钟。
方法二:画图理解题意。

由图可知,90分钟内张叔叔一共休息了10分钟。
方法三:可以把张叔叔每次竞走和休息的时间30 + 5 = 35(分)看作一个周期,看上午8时到上午9时30分里有几个35分,9时30分 - 8时 = 1时30分 = 90分,90÷35 = 2(个)……20(分),余的20分比30分短,所以张叔叔这20分都在竞走,而在2个35分里,张叔叔休息了2个5分,一共休息了2×5 = 10(分)。
所以张叔叔竞走的时间是90-5x2=80(分),再用“速度X时间”求出张叔叔一共竞走的路程。
完全解答:列表或画图见思路导引。
9时30分-8时=1时30分=90分
90÷35=2(个)…20(分)
100x(90-5x2)=8000(米)
答:张叔叔一共竞走了8000米
点评苑:用列表或画图的方法整理条件,可以弄清数量之间的关系,从而快速、正确地解决问题。
考点六 用假设的策略解决问题
例题6 停车场停放着一些自行车和面包车。两种车共14辆,有36个车轮。自行车和面包车分别有多少辆?
例题6 停车场停放着一些自行车和面包车。两种车共14辆,有36个车轮。自行车和面包车分别有多少辆?
答案:
思路导引:此题本质上属于“鸡兔同笼”问题。解题时可将题中的“自行车”“面包车”“车轮的总个数”“自行车与面包车的总辆数”分别与“鸡”“兔”“脚的总只数”“总头数”建立对应关系,这样就转化为标准的“鸡兔同笼”问题,然后用假设法解答。
完全解答:假设全部是自行车。
面包车:(36 - 2×14)÷(4 - 2)=4(辆)
自行车:14 - 4 = 10(辆)
答:自行车有10辆,面包车有4辆。
点评苑:用假设的策略解决问题时,要结合题中的数据,有目的地进行调整,从而更快地找到问题的答案。
完全解答:假设全部是自行车。
面包车:(36 - 2×14)÷(4 - 2)=4(辆)
自行车:14 - 4 = 10(辆)
答:自行车有10辆,面包车有4辆。
点评苑:用假设的策略解决问题时,要结合题中的数据,有目的地进行调整,从而更快地找到问题的答案。
考点七 用转化的策略解决问题
例题7 小明和小强在书店买了同样一本书。小明用去所带钱的$\frac{1}{2},$小强用去所带钱的$\frac{5}{6},$小明剩下的钱比小强多14元。小明原来带了多少元?
例题7 小明和小强在书店买了同样一本书。小明用去所带钱的$\frac{1}{2},$小强用去所带钱的$\frac{5}{6},$小明剩下的钱比小强多14元。小明原来带了多少元?
答案:
思路导引:根据“买了同样一本书。小明用去所带钱的$\frac{1}{2},$小强用去所带钱的$\frac{5}{6}”,$可以得到“小明所带的钱$×\frac{1}{2}=$小强所带的钱$×\frac{5}{6}”,$进而求出小明与小强所带的钱数的比。因为他们用去的钱一样多,所以可以将“小明剩下的钱比小强多14元”转化为小明原来的钱比小强多14元。最后按比例分配,求出小明原来带的钱数。
完全解答:小明所带的钱$×\frac{1}{2}=$小强所带的钱$×\frac{5}{6}$
小明所带的钱:小强所带的钱 = 5:3
14÷(5 - 3)×5 = 35(元)
答:小明原来带了35元。
点评苑:转化的策略在解决分数、百分数和比的实际问题中应用十分广泛,它可以简化数量关系,从而更方便、快捷地解题。
完全解答:小明所带的钱$×\frac{1}{2}=$小强所带的钱$×\frac{5}{6}$
小明所带的钱:小强所带的钱 = 5:3
14÷(5 - 3)×5 = 35(元)
答:小明原来带了35元。
点评苑:转化的策略在解决分数、百分数和比的实际问题中应用十分广泛,它可以简化数量关系,从而更方便、快捷地解题。
考点八 盈亏问题
例题8 小涵在文具超市看了一款钢笔和圆珠笔,1支钢笔比1支圆珠笔贵1.2元,小涵带的钱买5支钢笔差1.5元,买8支圆珠笔多0.6元。小涵带了多少元?
例题8 小涵在文具超市看了一款钢笔和圆珠笔,1支钢笔比1支圆珠笔贵1.2元,小涵带的钱买5支钢笔差1.5元,买8支圆珠笔多0.6元。小涵带了多少元?
答案:
思路导引:1支钢笔比1支圆珠笔贵1.2元,买5支钢笔差1.5元,那买5支圆珠笔就会多1.2×5 - 1.5 = 4.5(元),而买8支圆珠笔多0.6元,则买8 - 5 = 3(支)圆珠笔就需要4.5 - 0.6 = 3.9(元),所以1支圆珠笔的价格是3.9÷3 = 1.3(元)。再根据小涵带的钱买8支圆珠笔多0.6元求出小涵带的钱数。
完全解答:1.2×5 - 1.5 = 4.5(元)
(4.5 - 0.6)÷(8 - 5)=1.3(元)
8×1.3 + 0.6 = 11(元)
答:小涵带了11元。
点评苑:通常盈亏问题只涉及一种物品,可以用公式计算。本题有钢笔和圆珠笔两种物品,要想利用盈亏问题的公式计算,就必须将它们转化为同一种物品(钢笔或者圆珠笔)。
完全解答:1.2×5 - 1.5 = 4.5(元)
(4.5 - 0.6)÷(8 - 5)=1.3(元)
8×1.3 + 0.6 = 11(元)
答:小涵带了11元。
点评苑:通常盈亏问题只涉及一种物品,可以用公式计算。本题有钢笔和圆珠笔两种物品,要想利用盈亏问题的公式计算,就必须将它们转化为同一种物品(钢笔或者圆珠笔)。
考点九 解决稍复杂的行程问题
例题9 在一条2400米长的环形跑道上,两人同时从同一起点按顺时针方向跑,24分钟后相遇。若两人速度不变,还是从原出发点同时出发,其中一人改成按逆时针方向跑,则8分钟后相遇。两人的速度分别是多少?
例题9 在一条2400米长的环形跑道上,两人同时从同一起点按顺时针方向跑,24分钟后相遇。若两人速度不变,还是从原出发点同时出发,其中一人改成按逆时针方向跑,则8分钟后相遇。两人的速度分别是多少?
答案:
思路导引:在环形跑道上,两人同时从同一起点按顺时针方向跑,24分钟后相遇,说明24分钟里跑得快的人比跑得慢的人多跑一圈,即2400米,据此可以求出两人的速度差。
若一人改成按逆时针方向跑,则8分钟后相遇,说明两人8分钟一共跑了一圈,即2400米,据此可以求出两人的速度和。
再利用和差问题的解法求出两人的速度。
完全解答:速度差:2400÷24 = 100(米/分)
速度和:2400÷8 = 300(米/分)
快的:(300 + 100)÷2 = 200(米/分)
慢的:(300 - 100)÷2 = 100(米/分)
答:两人的速度分别是200米/分和100米/分。
点评苑:在环形跑道上同一起点,如果两人同时同向出发,那么第一次相遇时,快的人比慢的人多跑一圈,用“跑道一圈的长度÷追及时间 = 两人的速度差”;如果两人同时反向出发,那么第一次相遇时,两人一共跑了一圈,用“跑道一圈的长度÷相遇时间 = 两人的速度和”。
若一人改成按逆时针方向跑,则8分钟后相遇,说明两人8分钟一共跑了一圈,即2400米,据此可以求出两人的速度和。
再利用和差问题的解法求出两人的速度。
完全解答:速度差:2400÷24 = 100(米/分)
速度和:2400÷8 = 300(米/分)
快的:(300 + 100)÷2 = 200(米/分)
慢的:(300 - 100)÷2 = 100(米/分)
答:两人的速度分别是200米/分和100米/分。
点评苑:在环形跑道上同一起点,如果两人同时同向出发,那么第一次相遇时,快的人比慢的人多跑一圈,用“跑道一圈的长度÷追及时间 = 两人的速度差”;如果两人同时反向出发,那么第一次相遇时,两人一共跑了一圈,用“跑道一圈的长度÷相遇时间 = 两人的速度和”。
考点十 用画图的策略解决图形问题
例题10 有一个长方形鱼塘,鱼塘的长比宽多20米。如果把这个鱼塘扩建成一个最小的正方形,那么面积增加1600平方米。原来鱼塘的面积是多少平方米?有一块边长是8米的正方形草坪,草坪外围有一个1米宽的花圃,花圃里栽有牡丹花,每株占地1平方米。一共栽了多少株牡丹花?
例题10 有一个长方形鱼塘,鱼塘的长比宽多20米。如果把这个鱼塘扩建成一个最小的正方形,那么面积增加1600平方米。原来鱼塘的面积是多少平方米?有一块边长是8米的正方形草坪,草坪外围有一个1米宽的花圃,花圃里栽有牡丹花,每株占地1平方米。一共栽了多少株牡丹花?
答案:
思路导引:鱼塘是一个长方形,把它扩建成一个最小的正方形,只要把宽扩成和长相等即可(如图),涂色部分就是增加的1600平方米,据此先求出原长方形的长是1600÷20 = 80(米),再根据长和宽的关系求出宽,最后求出原来鱼塘的面积。

正方形草坪外围有一个1米宽的花圃,即在正方形四周向外延伸1米形成的“回”字形(如图),所以花圃外边长是8 + 1 + 1 = 10(米),外、内正方形的面积差就是花圃的面积,再看面积里包含多少个1平方米就能栽多少株牡丹花。
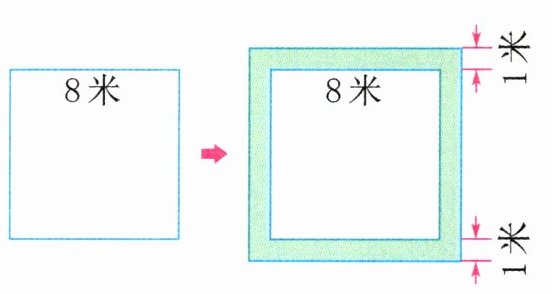
完全解答:1600÷20 = 80(米)
80×(80 - 20)=4800(平方米)
8 + 1 + 1 = 10(米)
10×10 - 8×8 = 36(平方米)
36÷1 = 36(株)
答:原来鱼塘的面积是4800平方米,花圃里一共栽了36株牡丹花。
点评苑:用画图法解决图形问题时,要看清题意,正确画图,才能找出正确的答案。
思路导引:鱼塘是一个长方形,把它扩建成一个最小的正方形,只要把宽扩成和长相等即可(如图),涂色部分就是增加的1600平方米,据此先求出原长方形的长是1600÷20 = 80(米),再根据长和宽的关系求出宽,最后求出原来鱼塘的面积。

正方形草坪外围有一个1米宽的花圃,即在正方形四周向外延伸1米形成的“回”字形(如图),所以花圃外边长是8 + 1 + 1 = 10(米),外、内正方形的面积差就是花圃的面积,再看面积里包含多少个1平方米就能栽多少株牡丹花。

完全解答:1600÷20 = 80(米)
80×(80 - 20)=4800(平方米)
8 + 1 + 1 = 10(米)
10×10 - 8×8 = 36(平方米)
36÷1 = 36(株)
答:原来鱼塘的面积是4800平方米,花圃里一共栽了36株牡丹花。
点评苑:用画图法解决图形问题时,要看清题意,正确画图,才能找出正确的答案。
考点十一 在变中抓不变解决问题
例题11 有两匹布,一匹长40米,另一匹长30米。把两匹布都剪去同样长的一部分后,发现短的那匹布剩余的长度是长的那匹布剩余长度的$\frac{3}{5}。$每匹布剪去了多少米?
例题11 有两匹布,一匹长40米,另一匹长30米。把两匹布都剪去同样长的一部分后,发现短的那匹布剩余的长度是长的那匹布剩余长度的$\frac{3}{5}。$每匹布剪去了多少米?
答案:
思路导引:本题中两匹布的长度是变量,把两匹布都剪去相同的长度后,长度差不变,还是40 - 30 = 10(米)。把长的那匹布剩下的长度看作单位“1”,10米对应的长度就是长的那匹布剩下长度的$(1 - \frac{3}{5}),$据此求出长的那匹布剩下的长度,再用“长的那匹布的长度 - 长的那匹布剩下的长度 = 剪去的长度”。
完全解答:$(40 - 30)÷(1 - \frac{3}{5})=25($米)
40 - 25 = 15(米)
答:每匹布剪去了15米。
点评苑:解决此类问题时,关键是找出题中的不变量及其对应的分率。
完全解答:$(40 - 30)÷(1 - \frac{3}{5})=25($米)
40 - 25 = 15(米)
答:每匹布剪去了15米。
点评苑:解决此类问题时,关键是找出题中的不变量及其对应的分率。
考点十二 用赋值法解决问题
例题12 狗跑5步的时间马可以跑3步,马跑4步的路程狗要跑7步。现在狗已经跑出30米,马开始追它。狗再跑多少米,马可以追上它?
例题12 狗跑5步的时间马可以跑3步,马跑4步的路程狗要跑7步。现在狗已经跑出30米,马开始追它。狗再跑多少米,马可以追上它?
答案:
思路导引:马跑1步的路程不知道,跑3步的时间也不知道,可以假设为具体数值,这样假设对解题结果没有影响。
完全解答:假设马跑1步的路程为7,则狗跑1步的路程为4;再假设马跑3步的时间为1,则狗跑5步的时间为1。
狗的速度:$4÷\frac{1}{5}=20$
马的速度:$7÷\frac{1}{3}=21$
20×[30÷(21 - 20)]=600(米)
答:狗再跑600米,马可以追上它。
点评苑:通过假设某一数量的具体值或特殊值,往往能简捷有效地解决一些问题,这种解题方法叫作赋值法。
完全解答:假设马跑1步的路程为7,则狗跑1步的路程为4;再假设马跑3步的时间为1,则狗跑5步的时间为1。
狗的速度:$4÷\frac{1}{5}=20$
马的速度:$7÷\frac{1}{3}=21$
20×[30÷(21 - 20)]=600(米)
答:狗再跑600米,马可以追上它。
点评苑:通过假设某一数量的具体值或特殊值,往往能简捷有效地解决一些问题,这种解题方法叫作赋值法。
教材思考题通解
有两支蜡烛,当第一支燃去$\frac{4}{5},$第二支燃去$\frac{2}{3}$时,剩下的部分一样长。这两支蜡烛原来长度的比是几比几?
有两支蜡烛,当第一支燃去$\frac{4}{5},$第二支燃去$\frac{2}{3}$时,剩下的部分一样长。这两支蜡烛原来长度的比是几比几?
答案:
思路导引:可以用多种策略解决问题。
(1) 画图法。
把两支蜡烛燃烧的情况用线段图表示出来,如图所示。

(2) 转化法。
先找出两支蜡烛剩下的部分,再比较。
第一支剩下$1 - \frac{4}{5}=\frac{1}{5},$第二支剩下$1 - \frac{2}{3}=\frac{1}{3},$那么第一支原来的长度$×\frac{1}{5}=$第二支原来的长度$×\frac{1}{3},$可以知道这两支蜡烛原来长度的比是5:3。
完全解答:这两支蜡烛原来长度的比是5:3。
思路导引:可以用多种策略解决问题。
(1) 画图法。
把两支蜡烛燃烧的情况用线段图表示出来,如图所示。

(2) 转化法。
先找出两支蜡烛剩下的部分,再比较。
第一支剩下$1 - \frac{4}{5}=\frac{1}{5},$第二支剩下$1 - \frac{2}{3}=\frac{1}{3},$那么第一支原来的长度$×\frac{1}{5}=$第二支原来的长度$×\frac{1}{3},$可以知道这两支蜡烛原来长度的比是5:3。
完全解答:这两支蜡烛原来长度的比是5:3。
查看更多完整答案,请扫码查看


