第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
3.(重点题)在〇里填“>”“<”或“=”。
500千克〇2吨
6000吨〇6千克
2000千克〇2吨
8500千克〇4吨
500千克〇2吨
6000吨〇6千克
2000千克〇2吨
8500千克〇4吨
答案:
< > = >
4.(重点题)选一选。
(1)一车煤重4000千克,一车纸重4吨,这车煤和这车纸相比,( )。
A. 煤重 B. 纸重 C. 一样重
(1)一车煤重4000千克,一车纸重4吨,这车煤和这车纸相比,( )。
A. 煤重 B. 纸重 C. 一样重
答案:
(1) C
(1) C
(2)与8头125千克的小牛的质量相等的是( )的质量。
A. 4袋25千克的面粉
B. 10桶100千克的大豆油
C. 6袋120千克的大米
A. 4袋25千克的面粉
B. 10桶100千克的大豆油
C. 6袋120千克的大米
答案:
(2) B
(2) B
5.(易错题)把各质量按从小到大的顺序排列。
1200千克 120克 12吨 3000千克
1200千克 120克 12吨 3000千克
答案:
120克<1200千克<3000千克<12吨
6.(变式题)工人叔叔准备用一辆载质量5吨的卡车一次运6台机器,每台机器重780千克。这辆卡车超载了吗?
答案:
$780×6 = 4680$(千克) 5吨 = 5000千克 4680<5000 没有超载
7.(重点题)有35吨沙子,先用一辆载质量8吨的卡车运走一车,剩下的用一辆载质量5吨的卡车运。还要运多少次才能运完?
答案:
$35 - 8 = 27$(吨) $27÷5 = 5$(次)……2(吨) $5 + 1 = 6$(次)
8.(创新题)2头大象和10头水牛一样重,2头水牛和4只老虎一样重。3头大象和多少只老虎一样重?
答案:
$10÷2 = 5$(头) $4÷2 = 2$(只) $3×5×2 = 30$(只)
9.(开放题)超市准备用载质量2吨的卡车进货(如图)。想一想,如果派两辆卡车,那么怎样装车才能一次运完,而且不超载?(用算式表示)


答案:
2吨 = 2000千克 方案一:① $1000 + 900 = 1900$(千克) ② $400 + 800 + 700 = 1900$(千克) 方案二:① $1000 + 800 = 1800$(千克) ② $400 + 900 + 700 = 2000$(千克)
10.(探究题)用2米和3米长的钢管焊接成一根22米长的管道,可以怎样选择?


答案:


知识百宝箱
知识点 用“画线段图”的策略解决问题
[教材第29页例2]

(1)买一套衣服要用多少元?
(2)买一件上衣比买一条裤子多用多少元?
知识点 用“画线段图”的策略解决问题
[教材第29页例2]

(1)买一套衣服要用多少元?
(2)买一件上衣比买一条裤子多用多少元?
答案:
(1)方法一:48×3=144(元)
(2)方法一:48×3=144(元)144-48=96(元)
(1)方法一:48×3=144(元)
144+48=192(元)
方法二:1+3=4(份)48×4=192(元)
答:买一套衣服要用 192元。
(2)方法一:48×3=144(元)144-48=96(元)
方法二:3-1=2(份)48×2=96(元)
答:买一件上衣比买一条裤子多用96元。
典例展示厅
类型一 年龄里的倍数问题
例题1 小敏今年12岁,6年前妈妈的年龄是小敏的5倍。妈妈今年多少岁?
类型一 年龄里的倍数问题
例题1 小敏今年12岁,6年前妈妈的年龄是小敏的5倍。妈妈今年多少岁?
答案:

思路导引:根据“6年前妈妈的年龄是
小敏的5倍”画出线段图如下:

6年前小敏12-6=6(岁),妈妈的年龄是她的5倍,也就是有5个6岁,即6x5-30(岁),妈妈今年的年龄比6年前增加了6岁,加上6岁就能得到妈妈今年的年龄。
完全解答:12-6=6(岁)
6x5=30(岁)
30+6=36(岁)
答:妈妈今年36岁
点评苑:随着年龄的不断增长,两人年龄之间的倍数关系会发生改变。
类型二 运用综合法或分析法解决实际问题
例题2 果园里有桃树、梨树、杏树和苹果树。苹果树有16棵,梨树的棵数是苹果树的2倍,桃树的棵数是梨树的3倍。
(1)桃树有多少棵?
(2)杏树的棵数比桃树的一半还少6,杏树有多少棵?
例题2 果园里有桃树、梨树、杏树和苹果树。苹果树有16棵,梨树的棵数是苹果树的2倍,桃树的棵数是梨树的3倍。
(1)桃树有多少棵?
(2)杏树的棵数比桃树的一半还少6,杏树有多少棵?
答案:
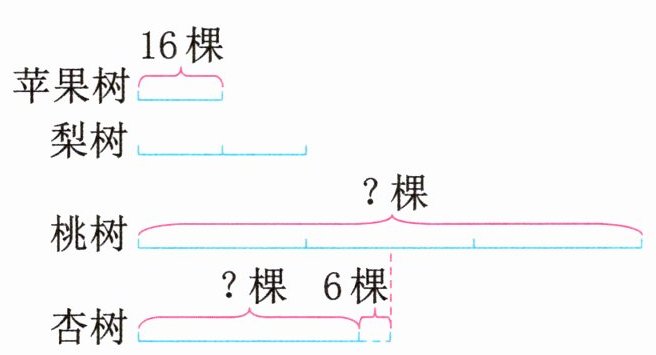
(2)96÷2=48(棵)
思路导引:根据题意,可以画出线段图
如下:

可以先求出梨树的棵数,再根据“桃树的棵数是梨树的3倍”,可以求出桃树的棵数。也可以从问题出发,要求桃树的棵数,就要知道梨树的棵数,而梨树的棵数又与苹果树的棵数有关,已知苹果树的棵数,即可一步一步地求出桃树的棵数。
完全解答:
(1)16x2-32(棵)
(1)16x2-32(棵)
32x3=96(棵)
答:桃树有96棵。
(2)96÷2=48(棵)
48-6=42(棵)
答:杏树有42棵。
点评苑:解决此类问题有两种不同的思路,从条件出发,根据已知条件逐步解决问题;从问题出发,分析要解决的问题需要什么条件,看条件是否具备,如果不具备,那么先求出间接条件,从而解决问题。
**考点一 与购票有关的实际问题**
**例题1** 张老师带9名书法社团的学生去参观书法展。他们购买门票最少需要多少元?
成人票:每张48元
儿童票:一律半价
团体票:每张25元(10人及以上)
**例题1** 张老师带9名书法社团的学生去参观书法展。他们购买门票最少需要多少元?
成人票:每张48元
儿童票:一律半价
团体票:每张25元(10人及以上)
答案:
方案一:48÷2 = 24(元)
24×9 = 216(元) 216 + 48 = 264(元)
方案二:1 + 9 = 10(人)
10×25 = 250(元) 250<264
答:他们购买门票最少需要250元。
24×9 = 216(元) 216 + 48 = 264(元)
方案二:1 + 9 = 10(人)
10×25 = 250(元) 250<264
答:他们购买门票最少需要250元。
**考点二 用“画线段图”的策略解决稍复杂的和倍问题**
**例题2** 甲、乙两堆沙子共150吨,已知甲堆沙子的质量比乙堆沙子质量的3倍多6吨,甲、乙两堆沙子各有多少吨?
**例题2** 甲、乙两堆沙子共150吨,已知甲堆沙子的质量比乙堆沙子质量的3倍多6吨,甲、乙两堆沙子各有多少吨?
答案:
**思路导引**:根据题意,画出线段图如下:
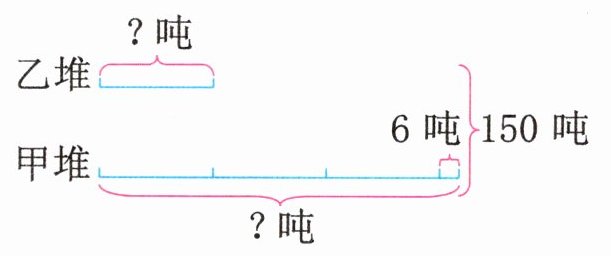
由上图可知,从150吨里去掉多的6吨,剩下的质量一共有4份,所以剩下的质量除以4就是乙堆沙子的质量,再用总质量减去乙堆沙子的质量就能得到甲堆沙子的质量。
**完全解答**:150 - 6 = 144(吨)
1 + 3 = 4(份) 144÷4 = 36(吨)
150 - 36 = 114(吨)
答:甲堆沙子有114吨,乙堆沙子有36吨。
**点评苑**:解答此类题先从总量里减去多余的数量,然后找出份数和所对应的具体数量是多少,求出一倍量,进而求另一个量。
**思路导引**:根据题意,画出线段图如下:

由上图可知,从150吨里去掉多的6吨,剩下的质量一共有4份,所以剩下的质量除以4就是乙堆沙子的质量,再用总质量减去乙堆沙子的质量就能得到甲堆沙子的质量。
**完全解答**:150 - 6 = 144(吨)
1 + 3 = 4(份) 144÷4 = 36(吨)
150 - 36 = 114(吨)
答:甲堆沙子有114吨,乙堆沙子有36吨。
**点评苑**:解答此类题先从总量里减去多余的数量,然后找出份数和所对应的具体数量是多少,求出一倍量,进而求另一个量。
**例题3** 丽丽和梅梅共有120本书,丽丽的本数比梅梅本数的3倍少4。丽丽和梅梅各有多少本书?
**思路导引**:根据题意,画出线段图如下:
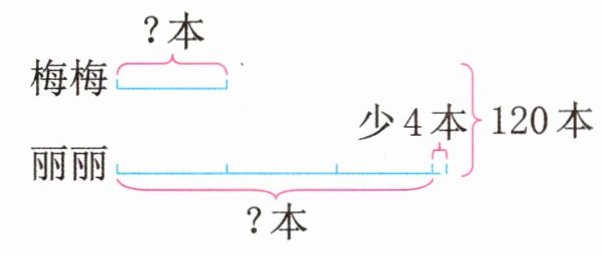
由上图可知,若丽丽增加4本,则丽丽的本数是梅梅的3倍,这时两人共有120 + 4 = 124(本),124本对应的是4份,先求出一份,即梅梅的本数,再用总本数减去梅梅的本数即可求出丽丽的本数。
**完全解答**:120 + 4 = 124(本)
1 + 3 = 4(份) 124÷4 = 31(本)
120 - 31 = 89(本)
答:丽丽有89本书,梅梅有31本书。
**点评苑**:解答此类题要注意先用总量加上缺少的数量,再根据“和倍问题”的解题思路进行解答。
**思路导引**:根据题意,画出线段图如下:

由上图可知,若丽丽增加4本,则丽丽的本数是梅梅的3倍,这时两人共有120 + 4 = 124(本),124本对应的是4份,先求出一份,即梅梅的本数,再用总本数减去梅梅的本数即可求出丽丽的本数。
**完全解答**:120 + 4 = 124(本)
1 + 3 = 4(份) 124÷4 = 31(本)
120 - 31 = 89(本)
答:丽丽有89本书,梅梅有31本书。
**点评苑**:解答此类题要注意先用总量加上缺少的数量,再根据“和倍问题”的解题思路进行解答。
答案:
**考点三 用“画线段图”的策略解决和差问题**
**例题4** 张奶奶家养了鸡和鸭共42只,其中鸡比鸭多12只。鸡有多少只?鸭有多少只?
**例题4** 张奶奶家养了鸡和鸭共42只,其中鸡比鸭多12只。鸡有多少只?鸭有多少只?
答案:
**思路导引**:根据题意,画出线段图如下:
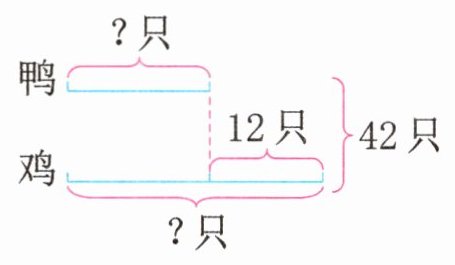
由上图可知,鸭的只数的2倍是42 - 12 = 30,先求出鸭的只数,再求出鸡的只数。也可以这样想:鸭的只数加上12就和鸡一样多,也就是鸡的只数的2倍是42 + 12 = 54,从而求出鸡的只数,进而求出鸭的只数。
**完全解答**:方法一:42 - 12 = 30(只)
30÷2 = 15(只) 15 + 12 = 27(只)
方法二:42 + 12 = 54(只)
54÷2 = 27(只)
27 - 12 = 15(只)
答:鸡有27只,鸭有15只。
**点评苑**:一般的和差问题是指已知两个量的和与差,分别要求这两个量是多少。解题的方法:(和 + 差)÷2 = 较大数,(和 - 差)÷2 = 较小数。
**思路导引**:根据题意,画出线段图如下:

由上图可知,鸭的只数的2倍是42 - 12 = 30,先求出鸭的只数,再求出鸡的只数。也可以这样想:鸭的只数加上12就和鸡一样多,也就是鸡的只数的2倍是42 + 12 = 54,从而求出鸡的只数,进而求出鸭的只数。
**完全解答**:方法一:42 - 12 = 30(只)
30÷2 = 15(只) 15 + 12 = 27(只)
方法二:42 + 12 = 54(只)
54÷2 = 27(只)
27 - 12 = 15(只)
答:鸡有27只,鸭有15只。
**点评苑**:一般的和差问题是指已知两个量的和与差,分别要求这两个量是多少。解题的方法:(和 + 差)÷2 = 较大数,(和 - 差)÷2 = 较小数。
**例题5** 三年级共有152人,每周四下午分成4个社团上课,美术社团比书法社团多16人,合唱社团比书法社团多20人,足球社团比书法社团少12人。四个社团分别有多少人?
答案:
**思路导引**:根据题意,画出线段图如下:

从图中可以看出(152 - 16 - 20 + 12)就是书法社团人数的4倍。先求出书法社团的人数,再根据其他数量关系逐步求出其余三个社团的人数。
**完全解答**:152 - 16 - 20 + 12 = 128(人)
128÷4 = 32(人)
32 + 16 = 48(人)
32 + 20 = 52(人)
32 - 12 = 20(人)
答:书法社团有32人,美术社团有48人,合唱社团有52人,足球社团有20人。
**点评苑**:解决多个数量相比较的和差问题时,一定要弄清楚以谁为标准,然后以此为突破口找出数量关系解决问题。
**思路导引**:根据题意,画出线段图如下:

从图中可以看出(152 - 16 - 20 + 12)就是书法社团人数的4倍。先求出书法社团的人数,再根据其他数量关系逐步求出其余三个社团的人数。
**完全解答**:152 - 16 - 20 + 12 = 128(人)
128÷4 = 32(人)
32 + 16 = 48(人)
32 + 20 = 52(人)
32 - 12 = 20(人)
答:书法社团有32人,美术社团有48人,合唱社团有52人,足球社团有20人。
**点评苑**:解决多个数量相比较的和差问题时,一定要弄清楚以谁为标准,然后以此为突破口找出数量关系解决问题。
**考点四 运用推理法解决付款问题**
**例题6** 3人去文具店买同样的练习本。到店后,丽丽发现没带钱,于是梅梅买了8本,红红买了7本。回来后三人决定平分这些练习本,且平均承担买练习本的费用。这样丽丽需要拿出20元,梅梅和红红分别需要收回多少元?
**例题6** 3人去文具店买同样的练习本。到店后,丽丽发现没带钱,于是梅梅买了8本,红红买了7本。回来后三人决定平分这些练习本,且平均承担买练习本的费用。这样丽丽需要拿出20元,梅梅和红红分别需要收回多少元?
答案:
**思路导引**:根据题意可知,三人平分了这些练习本,共8 + 7 = 15(本),所以每人分得15÷3 = 5(本)。因为买的是同样的练习本,所以3个人应付的钱数也应该一样多,都是20元。根据题意可以列出数量关系如下:
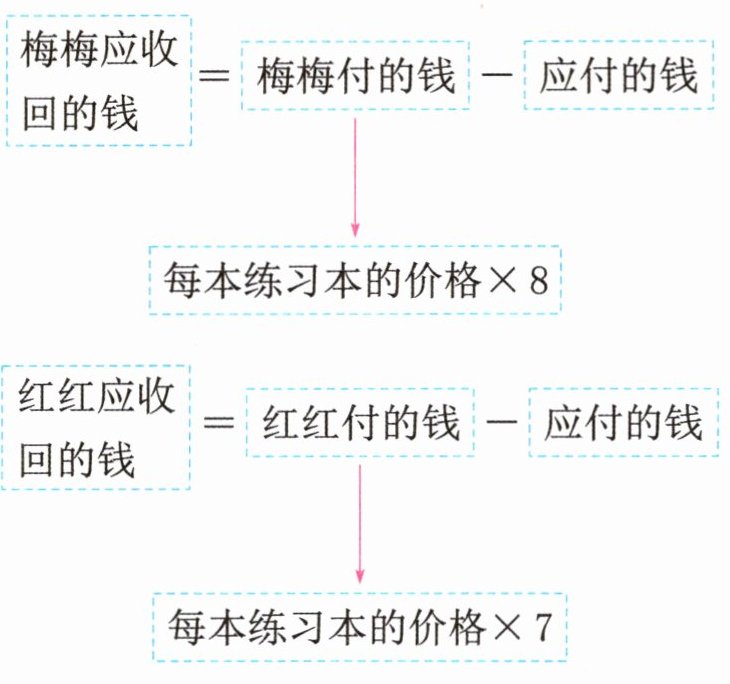
先求出每本练习本的价格,再根据数量关系即可求解。
**完全解答**:8 + 7 = 15(本)
15÷3 = 5(本)
20÷5 = 4(元)
4×8 = 32(元)
32 - 20 = 12(元)
4×7 = 28(元)
28 - 20 = 8(元)
答:梅梅需要收回12元,红红需要收回8元。
**点评苑**:解决此题的关键在于先求出每本练习本的价格。从问题出发,分析解决问题所需的数量关系,再联系已知条件进行解答。
**思路导引**:根据题意可知,三人平分了这些练习本,共8 + 7 = 15(本),所以每人分得15÷3 = 5(本)。因为买的是同样的练习本,所以3个人应付的钱数也应该一样多,都是20元。根据题意可以列出数量关系如下:

先求出每本练习本的价格,再根据数量关系即可求解。
**完全解答**:8 + 7 = 15(本)
15÷3 = 5(本)
20÷5 = 4(元)
4×8 = 32(元)
32 - 20 = 12(元)
4×7 = 28(元)
28 - 20 = 8(元)
答:梅梅需要收回12元,红红需要收回8元。
**点评苑**:解决此题的关键在于先求出每本练习本的价格。从问题出发,分析解决问题所需的数量关系,再联系已知条件进行解答。
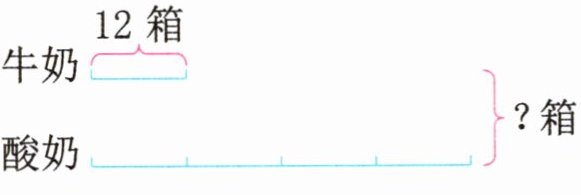
**三、看图列式计算。(每题5分,共10分)**
1.
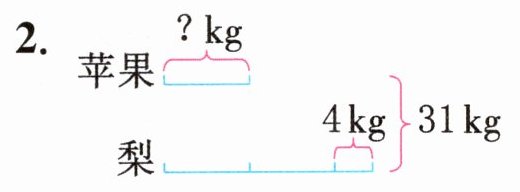
1.


答案:
1. 12×4 = 48(箱) 12 + 48 = 60(箱)
@@2. 31 - 4 = 27(kg) 1 + 2 = 3(份) 27÷3 = 9(kg)
@@2. 31 - 4 = 27(kg) 1 + 2 = 3(份) 27÷3 = 9(kg)
2. 三个笼子里共有18只兔子,如果从第一个笼子里取出4只放到第二个笼子里,再从第二个笼子里取出3只放到第三个笼子里,这样三个笼子里的兔子就一样多了。三个笼子里原来分别有多少只兔子?
答案:
2. $18\div3 = 6$(只) 第一个笼子:$6 + 4 = 10$(只) 第二个笼子:$6 + 3 - 4 = 5$(只) 第三个笼子:$6 - 3 = 3$(只)
查看更多完整答案,请扫码查看


