《2025年通城学典非常课课通三年级数学下册苏教版》

考点一 计算不规则图形的面积
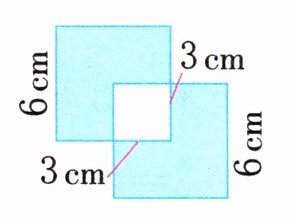
例题1 下图是由两个边长6 cm的大正方形组成的，它们重叠的部分是边长3 cm的小正方形。涂色部分的面积是多少平方厘米？

答案： $6×6 = 36(cm^{2})$ $3×3 = 9(cm^{2})$ $(36 - 9)×2 = 54(cm^{2})$
答：涂色部分的面积是$54 cm^{2}$。

考点二 从不同角度解决面积问题
例题2 如右图，有一块长20米、宽15米的长方形草地，在它的四周向外修筑一条宽2米的小路。小路的面积是多少平方米？

答案： 方法一：20＋2＋2＝24(米) 15＋2＋2＝19(米) 24×19＝456(平方米) 20×15＝300(平方米) 456－300＝156(平方米)
方法二：20＋2＋2＝24(米) 24×2＝48(平方米) 15×2＝30(平方米) (48＋30)×2＝156(平方米)
答：小路的面积是156平方米。

考点三 运用假设法解决有关面积和周长的问题
例题3 若一个长方形的长扩大到原来的3倍，宽也扩大到原来的3倍，则这个长方形的面积扩大到原来的( )倍，周长扩大到原来的( )倍。

答案： 9 3

考点四 解决生活中稍复杂的面积问题
例题4 学校举行绘画比赛，参赛作品的形状都是边长30厘米的正方形，现准备把这些作品展示出来。一块长方形展板上每行放8幅作品，正好能放满4行(不考虑作品之间的空隙)，这块长方形展板的面积是多少平方分米？

答案： 30厘米＝3分米
方法一：8×3＝24(分米) 4×3＝12(分米) 24×12＝288(平方分米)
方法二：3×3＝9(平方分米) 8×4＝32(幅) 32×9＝288(平方分米)
答：这块长方形展板的面积是288平方分米。

教材思考题通解 [教材P75]
青湾村有一个正方形养鱼池，在养鱼池的四角都栽有一棵树。现在要扩大养鱼池，扩大后养鱼池的形状仍然是正方形，面积是原来的2倍。不移动这4棵树，能做到吗？

答案：

1. 在括号里填合适的单位。
一块展板的面积大约是45( )。
一块正方形鼠标垫的边长是20( )，面积是4( )。
舞蹈房的面积大约是80( )。
两个小朋友面对面抱在一起，他们站在地上的面积大约是8( )。

答案： 平方分米 厘米 平方分米 平方米 平方分米

2. 一张边长80 cm的方桌，面积是( )$cm^{2}$，是( )$dm^{2}$。

答案： 6400 64

3. 6平方分米＝( )平方厘米
2300平方分米＝( )平方米
7平方米＝( )平方分米
4000米＝( )千米

答案： 600 23 700 4

4. 一块长方形菜地的长是8米，宽是5米，面积是( )平方米，是( )平方分米。

答案： 40 4000

5. 用两个边长4 cm的正方形拼成一个长方形，这个长方形的周长是( )cm，面积是( )$cm^{2}$。

答案： 24 32

6. 将一块正方形稻田的边长扩大到原来的2倍，扩大后稻田的周长是原来的( )倍，面积是原来的( )倍。

答案： 2 4

7. 一个长方形保鲜袋的长是30 cm，宽是20 cm。做一个这样的保鲜袋至少需要用塑料薄膜( )$dm^{2}$。

答案： 12

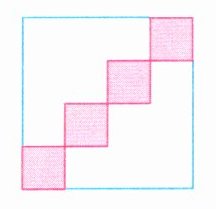
8. 下图中每个小正方形的边长是1厘米，大正方形的面积是( )平方厘米。

答案： 16

9. 工人师傅想在一个边长4米的正方形水池的外围铺一条宽1米的小路，小路的面积是( )平方米。

答案： 20

1. 用一根长20米的铁丝围成一个最大的正方形，它的面积是( )。
A. 25米
B. 20平方米
C. 25平方米

答案： C

2. 一块长方形菜地的长是10 m，宽是长的一半，菜地的面积是( )$m^{2}$。
A. 20
B. 50
C. 200

答案： B

3. 用16个相同的小正方形依次拼成两个大长方形，这两个大长方形的面积( )。
A. 一样大
B. 不一样大
C. 无法比较

答案： A

4. 如图，长方形被分成了甲、乙两部分，这两部分的( )。


A. 周长和面积都不相等
B. 周长相等，面积不相等
C. 面积相等，周长不相等

答案： A

5. 张伯伯用篱笆围了一个面积是40平方米的长方形月季园。如果月季园的长、宽均是整米数，那么月季园的周长不可能是( )米。
A. 44
B. 82
C. 36

答案： C

三、求下面图形的周长和面积。(共8分)

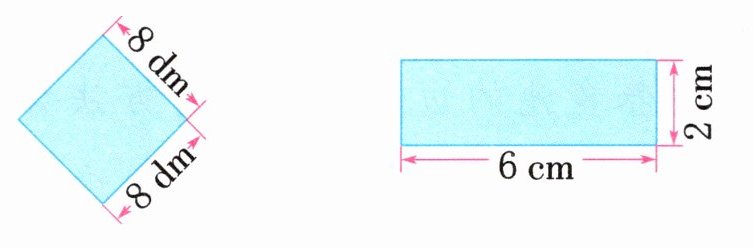
答案： 周长：$8×4 = 32(dm)$ 面积：$8×8 = 64(dm^{2})$
周长：$(6 + 2)×2 = 16(cm)$ 面积：$6×2 = 12(cm^{2})$

1. 下面每个小方格表示1平方厘米。

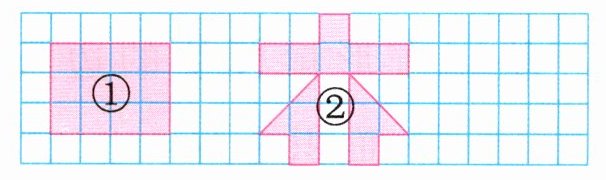
(1) 把图形①分成一个正方形和一个长方形，图②的面积是( )平方厘米。(4分)
(2) 在方格图中画一个面积是8平方厘米的图形。(2分)

答案： （1）图略 12 （2）略

2. 一个长方形花圃，每条边的中间有一棵树(如下图)。现要将花圃的面积缩小一半，且保留原来的4棵树，可以怎么变化？画一画。(3分)

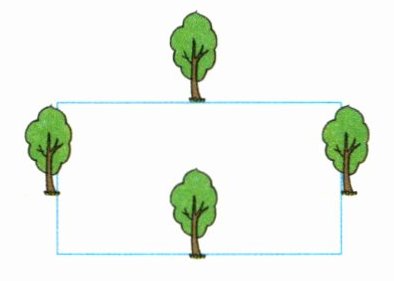
答案：

1. 要给下面这幅画配上一块玻璃封面，至少需要多少平方厘米的玻璃？是多少平方分米？(4分)

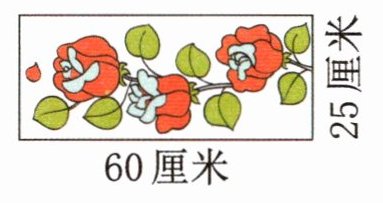
答案： $60×25 = 1500$(平方厘米) 1500平方厘米 = 15平方分米

2. 一块正方形菜地的边长是20米。
(1) 给这块菜地的四周围上篱笆，篱笆长多少米？(3分)
(2) 如果每平方米菜地可以收获青菜9千克，那么这块菜地一共可以收获青菜多少千克？(3分)

答案： （1）$20×4 = 80$(米)
（2）$20×20 = 400$(平方米) $400×9 = 3600$(千克)

3. 一面面积为70平方米的墙上有5扇小窗，每扇小窗的面积为40平方分米。如果要粉刷这面墙，那么粉刷的面积是多少平方米？(4分)

答案： $40×5 = 200$(平方分米) 200平方分米 = 2平方米 $70 - 2 = 68$(平方米)

4. 一个长方形林场，长是70米，是宽的2倍。这个林场的面积是多少平方米？(4分)

答案： $70÷2 = 35$(米) $70×35 = 2450$(平方米)

5. 李爷爷用篱笆靠墙围了一个长方形鸡舍(如下图)，篱笆长22米。鸡舍的面积是多少平方米？(5分)

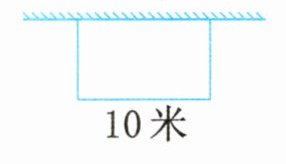
答案： $(22 - 10)÷2 = 6$(米) $10×6 = 60$(平方米)

6. 如图，街心花园中有一个正方形花坛，花坛四周有1米宽的水泥路。若水泥路的总面积是12平方米，则中间花坛的面积是多少平方米？(5分)

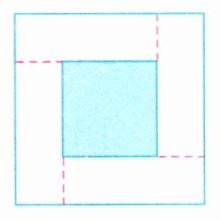
答案： $12÷4 = 3$(平方米) $3÷1 = 3$(米) $3 - 1 = 2$(米) $2×2 = 4$(平方米)