(17)(本大题满分12分)
设函数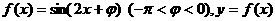 图像的一条对称轴是直线
图像的一条对称轴是直线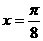 。
。
(Ⅰ)求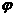 ;
;
(Ⅱ)求函数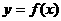 的单调增区间;
的单调增区间;
(Ⅲ)画出函数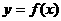 在区间
在区间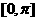 上的图像。
上的图像。
(18)(本大题满分12分)
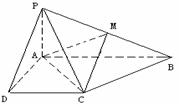
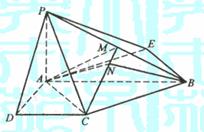
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,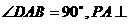 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=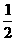 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小。
(19)(本大题满分12分)
已知二次函数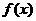 的二次项系数为
的二次项系数为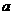 ,且不等式
,且不等式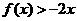 的解集为
的解集为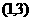 。
。
(Ⅰ)若方程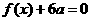 有两个相等的根,求
有两个相等的根,求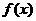 的解析式;
的解析式;
(Ⅱ)若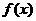 的最大值为正数,求
的最大值为正数,求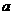 的取值范围。
的取值范围。
(20)(本大题满分12分)
9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为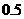 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
(Ⅰ)求甲坑不需要补种的概率;
(Ⅱ)求3个坑中恰有1个坑不需要补种的概率;
(Ⅲ)求有坑需要补种的概率。
(精确到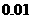 )
)
(21)(本大题满分12分)
设正项等比数列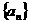 的首项
的首项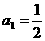 ,前n项和为
,前n项和为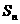 ,且
,且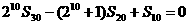 。
。
(Ⅰ)求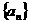 的通项;
的通项;
(Ⅱ)求 的前n项和
的前n项和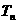 。
。
(22)(本大题满分14分)
已知椭圆的中心为坐标原点O,焦点在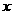 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,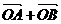 与
与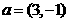 共线。
共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且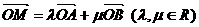 ,证明
,证明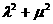 为定值。
为定值。






(13)若正整数m满足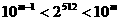 ,则m = 。
,则m = 。
解:∵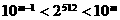 ,∴
,∴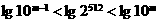 ,即
,即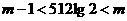 ,
,
∴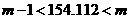 ,即
,即 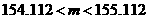 ,∴
,∴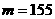 .
.
(14)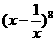 的展开式中,常数项为
。(用数字作答
的展开式中,常数项为
。(用数字作答
解: 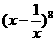 的通项公式为
的通项公式为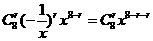 ,令8-2r=0,得r=4,∴常数项为70.
,令8-2r=0,得r=4,∴常数项为70.
(15)从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有 种。
解:用剔除法.: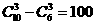 ,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。
,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。
(16)在正方形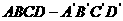 中,过对角线
中,过对角线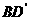 的一个平面交
的一个平面交 于E,交
于E,交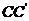 于F,
于F,
①
四边形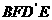 一定是平行四边形
一定是平行四边形
②
四边形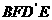 有可能是正方形
有可能是正方形
③
四边形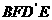 在底面ABCD内的投影一定是正方形
在底面ABCD内的投影一定是正方形
④
四边形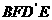 有可能垂直于平面
有可能垂直于平面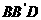
以上结论正确的为 。(写出所有正确结论的编号)
 解:①平面
解:①平面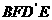 与相对侧面相交,交线互相平行,
与相对侧面相交,交线互相平行,
∴四边形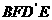 一定是平行四边形;
一定是平行四边形;
②四边形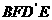 若是正方形,则
若是正方形,则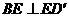 ,又
,又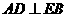 ,
,
∴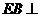 平面
平面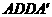 ,产生矛盾;
,产生矛盾;
③四边形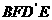 在底面ABCD内的投影是正方形
在底面ABCD内的投影是正方形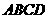 ;
;
④当E、F分别是 、
、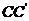 的中点时,
的中点时,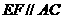 ,又
,又 平面
平面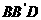 ,
,
∴四边形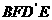 有可能垂直于平面,∴填①③④.
有可能垂直于平面,∴填①③④.
(1)设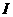 为全集,
为全集,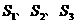 是
是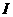 的三个非空子集,且
的三个非空子集,且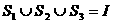 ,则下面论断正确的是
,则下面论断正确的是
(A)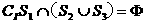 (B)
(B)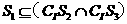
 (C)
(C)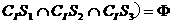 (D)
(D)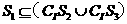
解:∵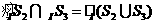 所表示的部分是图中蓝色
所表示的部分是图中蓝色
的部分,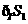 所表示的部分是图中除去
所表示的部分是图中除去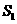 的部分,
的部分,
∴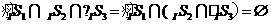 ,故选C.
,故选C.
(2)一个与球心距离为1的平面截球所得的圆面面积为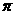 ,则球的表面积为
,则球的表面积为
(A)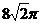 (B)
(B)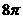 (C)
(C)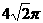 (D)
(D)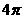
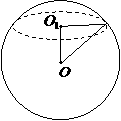 解:∵截面圆面积为
解:∵截面圆面积为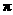 ,∴截面圆半径
,∴截面圆半径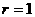 ,
,
∴球的半径为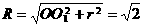 ,
,
∴球的表面积为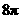 ,故选B.
,故选B.
(3)函数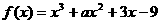 ,已知
,已知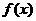 在
在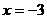 时取得极值,则
时取得极值,则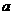 =
=
(A)2 (B)3 (C)4 (D)5
解: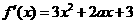 ,令
,令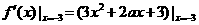 =0,解得a=5,选(D)
=0,解得a=5,选(D)
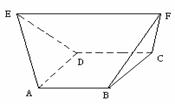
(4)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且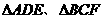 均为正三角形,EF∥AB,EF=2,则该多面体的体积为
均为正三角形,EF∥AB,EF=2,则该多面体的体积为
 (A)
(A)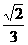 (B)
(B)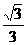
(C) (D)
(D)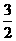
解:如图,过A、B两点分别作AM、BN垂直于EF,垂足分别为M、N,连结DM、CN,可证得DM⊥EF、CN⊥EF,多面体ABCDEF分为三部分,多面体的体积V为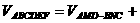
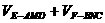 ,∵
,∵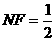 ,
,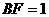 ,∴
,∴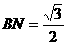 ,
,
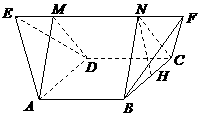 作NH垂直于点H,则H为BC的中点,则
作NH垂直于点H,则H为BC的中点,则 ,∴
,∴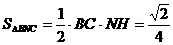 ,∴
,∴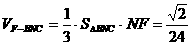 ,
,
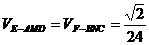 ,
,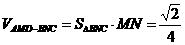 ,∴
,∴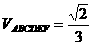 ,故选A.
,故选A.
(5)已知双曲线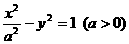 的一条准线为
的一条准线为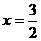 ,则该双曲线的离心率为
,则该双曲线的离心率为
(A)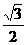 (B)
(B)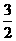 (C)
(C)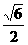 (D)
(D)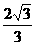
解:由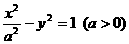 得
得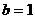 ,∴
,∴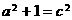 ,抛物线
,抛物线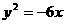 的准线为
的准线为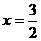 ,因为双曲线
,因为双曲线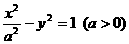 的一条准线与抛物线
的一条准线与抛物线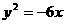 的准线重合,所以
的准线重合,所以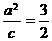 ,解得
,解得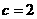 ,所以
,所以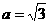 ,所以离心率为
,所以离心率为 ,故选D.
,故选D.
(6)当 时,函数
时,函数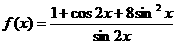 的最小值为
的最小值为
(A)2 (B)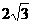 (C)4 (D)
(C)4 (D)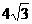
解: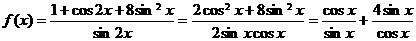
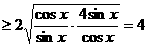 ,当且仅当
,当且仅当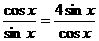 ,即
,即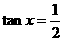 时,取“
时,取“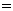 ”,∵
”,∵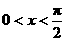 ,∴存在
,∴存在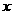 使
使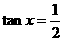 ,这时
,这时 ,故选(C).
,故选(C).
(7)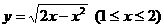 反函数是
反函数是
(A)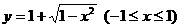
(B)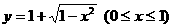
(C)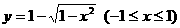
(D)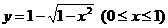
解:由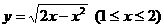 ,得
,得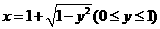 ,故
,故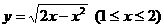 的反函数为
的反函数为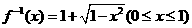 ,选(D)
,选(D)
(8)设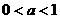 ,函数
,函数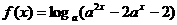 ,则使
,则使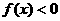 的
的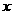 的取值范围是
的取值范围是
(A)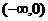 (B)
(B)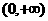 (C)
(C)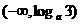 (D)
(D)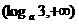
解:∵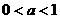 ,
,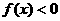 ,∴
,∴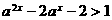 ,解得
,解得 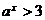 或
或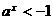 (舍去),
(舍去),
∴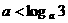 ,故选C.
,故选C.
(9)在坐标平面上,不等式组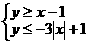 所表示的平面区域的面积为
所表示的平面区域的面积为
(A)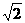 (B)
(B)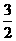 (C)
(C)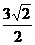 (D)2
(D)2
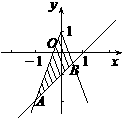 解:原不等式化为
解:原不等式化为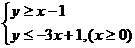 或
或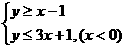 ,
,
所表示的平面区域如右图所示, ,
,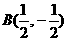 ,
,
∴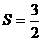 ,故选B
,故选B
(10)在 中,已知
中,已知 ,给出以下四个论断:
,给出以下四个论断:
①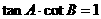 ②
②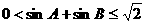
③ ④
④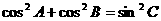
其中正确的是
(A)①③ (B)②④ (C)①④ (D)②③
解:∵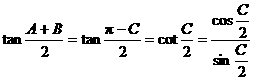 ,
,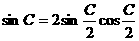 ,
,
∴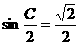 ,∴
,∴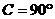 ,
,
∵ ,∴①不一定成立,
,∴①不一定成立,
∵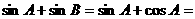
 ,∴
,∴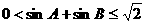 ,∴②成立,
,∴②成立,
∵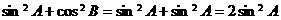 ,∴③不一定成立,
,∴③不一定成立,
∵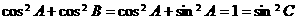 ,∴④成立,故选B.
,∴④成立,故选B.
(11)点O是三角形ABC所在平面内的一点,满足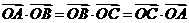 ,则点O是
,则点O是 的
的
(A)三个内角的角平分线的交点 (B)三条边的垂直平分线的交点 (C)三条中线的交点 (D)三条高的交点
解: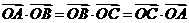 ,即
,即
得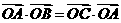 ,
,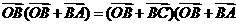
即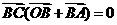 ,故
,故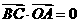 ,
,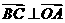 ,同理可证
,同理可证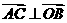 ,∴O是
,∴O是 的三条高的交点,选(D)
的三条高的交点,选(D)
(12)设直线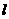 过点
过点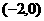 ,且与圆
,且与圆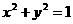 相切,则
相切,则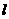 的斜率是
的斜率是
(A)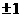 (B)
(B)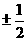 (C)
(C)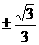 (D)
(D)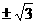
解:设过点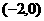 ,且与圆
,且与圆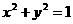 相切的直线
相切的直线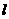 的斜率为k,则直线
的斜率为k,则直线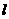 的方程为:y-kx+2k=0,k满足:1=
的方程为:y-kx+2k=0,k满足:1=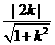 得k=
得k=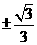 ,选(D).
,选(D).
第Ⅱ卷
22.本小题主要考查数学归纳法及导数应用等知识,考查综合运用数学知识解决问题的能力.
满分12分.
(Ⅰ)解:对函数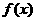 求导数:
求导数: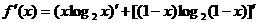


于是
当 在区间
在区间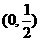 是减函数,
是减函数,
当 在区间
在区间 是增函数.
是增函数.
所以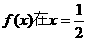 时取得最小值,
时取得最小值,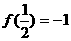 ,
,
(Ⅱ)证法一:用数学归纳法证明.
(i)当n=1时,由(Ⅰ)知命题成立.
(ii)假定当 时命题成立,即若正数
时命题成立,即若正数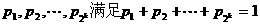 ,
,
则
当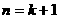 时,若正数
时,若正数
令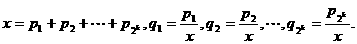
则 为正数,且
为正数,且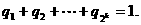
由归纳假定知

 ①
①
同理,由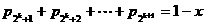 可得
可得
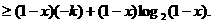 ②
②
综合①、②两式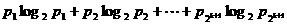
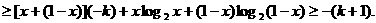
即当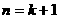 时命题也成立.
时命题也成立.
根据(i)、(ii)可知对一切正整数n命题成立.
证法二:
令函数
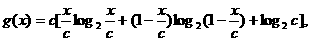
利用(Ⅰ)知,当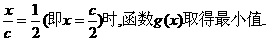
对任意
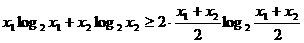
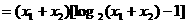 . ①
. ①
下面用数学归纳法证明结论.
(i)当n=1时,由(I)知命题成立.
(ii)设当n=k时命题成立,即若正数

由①得到
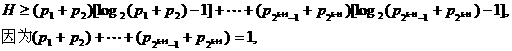
由归纳法假设
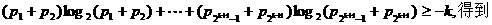

即当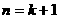 时命题也成立.
时命题也成立.
所以对一切正整数n命题成立.
21.本小题主要考查直线方程、平面向量及椭圆的几何性质等基本知训,考查综合运用数学知识解决问题及推理的能力,满分14分.
(I)解:设椭圆方程为
则直线AB的方程为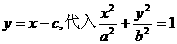
化简得 .
.
令
则 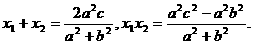

 共线,得
共线,得


(II)证明:由(I)知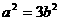 ,所以椭圆
,所以椭圆 可化为
可化为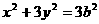 .
.
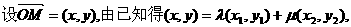

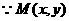 在椭圆上,
在椭圆上,

即  ①
①
由(I)知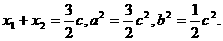
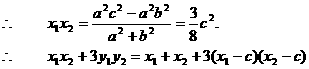
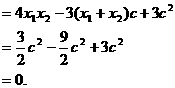
又 又,代入①得
又,代入①得 
故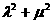 为定值,定值为1.
为定值,定值为1.
20.本小题主要考查相互独立事件和互斥事件有一个发生的概率的计算方法,考查运用概率
知识解决实际问题的能力. 满分12分.
(Ⅰ)解:因为甲坑内的3粒种子都不发芽的概率为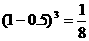 ,所以甲坑不需要补
,所以甲坑不需要补
种的概率为 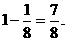
3个坑都不需要补种的概率
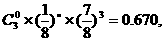
恰有1个坑需要补种的概率为
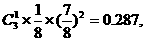
恰有2个坑需要补种的概率为
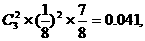
3个坑都需要补种的概率为

补种费用 的分布为
的分布为
 |
0 |
10 |
20 |
30 |
|
P |
0.670 |
0.287 |
0.041 |
0.002 |
 的数学期望为
的数学期望为
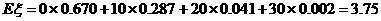
19. 本小题主要考查等比数列的基本知识,考查分析问题能力和推理能力,满分12分.
解:(Ⅰ)因为 是等比数列,
是等比数列,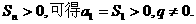
当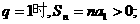

上式等价于不等式组: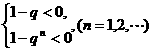 ①
①
或 ②
②
解①式得q>1;解②,由于n可为奇数、可为偶数,得-1<q<1.
综上,q的取值范围是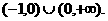
(Ⅱ)由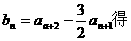

于是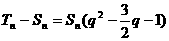
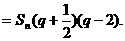
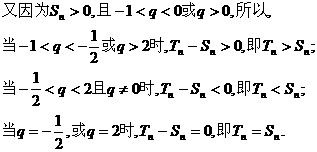
18.本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分12分.
 方案一:
方案一:
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连结AE,可知AC=CB=BE=AE= ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE= ,PB=
,PB= ,
, 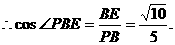

(Ⅲ)解:作AN⊥CM,垂足为N,连结BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角.
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC= ,
,
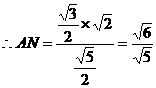 . ∴AB=2,
. ∴AB=2,
故所求的二面角的大小为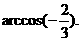
方法二:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为
A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1, .
.
(Ⅰ)证明:因
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD.
 (Ⅱ)解:因
(Ⅱ)解:因
则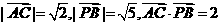 ,
,
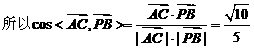 .
.
故AC与PB所成的角的大小为
(Ⅲ)解:在MC上取一点N(x,y,z),则存在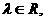 使
使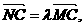

要使
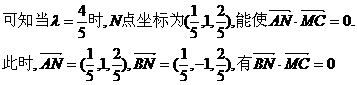
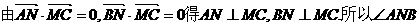 为所求二面角的平面角.
为所求二面角的平面角.

(本题也可通过求两个平面的法向量所成角来确定二面角的平面角)
17.本小题主要考查三角函数性质及图像的基本知识,考查推理和运算能力,满分12分.
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,
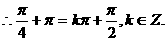
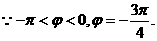
(Ⅱ)由(Ⅰ)知
由题意得

所以函数
(Ⅲ)证明:
所以曲线 的切线斜率取值范围为[-2,2],而直线
的切线斜率取值范围为[-2,2],而直线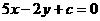 的斜率为
的斜率为 ,所以直线
,所以直线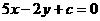 与函数
与函数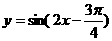 的图像不相切.
的图像不相切.
(17)(本大题满分12分)
设函数 图像的一条对称轴是直线
图像的一条对称轴是直线 .
.
(Ⅰ)求 ;
;
(Ⅱ)求函数 的单调增区间;
的单调增区间;
(Ⅲ)证明直线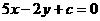 于函数
于函数 的图像不相切.
的图像不相切.
(18)(本大题满分12分)
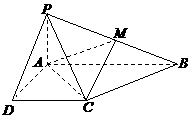 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,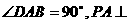 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC= AB=1,M是PB的中点.
AB=1,M是PB的中点.
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小.
(19)(本大题满分12分)
设等比数列 的公比为
的公比为 ,前n项和
,前n项和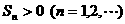 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设 ,记
,记 的前n项和为
的前n项和为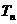 ,试比较
,试比较 与
与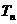 的大小.
的大小.
(20)(本大题满分12分)
9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种.假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种.假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到 )
)
(21)(本大题满分14分)
已知椭圆的中心为坐标原点O,焦点在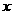 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点, 与
与 共线.
共线.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且 ,证明
,证明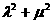 为定值.
为定值.
(22)(本大题满分12分)
(Ⅰ)设函数 ,求
,求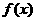 的最小值;
的最小值;
(Ⅱ)设正数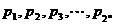 满足
满足 ,证明:
,证明:


