(17)(本大题满分12分)
设函数 图像的一条对称轴是直线
图像的一条对称轴是直线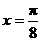 .
.
(Ⅰ)求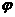 ;
;
(Ⅱ)求函数 的单调增区间;
的单调增区间;
(Ⅲ)证明直线 于函数
于函数 的图像不相切.
的图像不相切.
(18)(本大题满分12分)
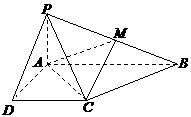 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,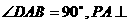 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=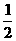 AB=1,M是PB的中点.
AB=1,M是PB的中点.
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小.
(19)(本大题满分12分)
设等比数列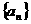 的公比为
的公比为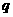 ,前n项和
,前n项和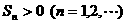 .
.
(Ⅰ)求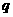 的取值范围;
的取值范围;
(Ⅱ)设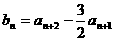 ,记
,记 的前n项和为
的前n项和为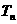 ,试比较
,试比较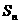 与
与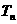 的大小.
的大小.
(20)(本大题满分12分)
9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为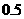 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种.假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种.假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到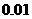 )
)
(21)(本大题满分14分)
已知椭圆的中心为坐标原点O,焦点在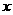 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,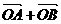 与
与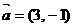 共线.
共线.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且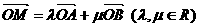 ,证明
,证明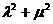 为定值.
为定值.
(22)(本大题满分12分)
(Ⅰ)设函数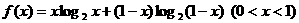 ,求
,求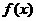 的最小值;
的最小值;
(Ⅱ)设正数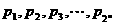 满足
满足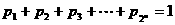 ,证明:
,证明:
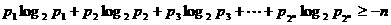
- 答案

