11.在△OAB中,O为坐标原点,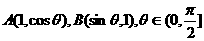 ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,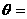 ( )
( )
A. B.
B.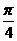 C.
C.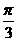 D.
D.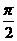
见理科卷11
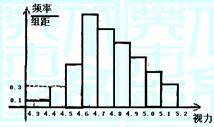 12.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
12.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
A.0,27,78 B.0,27,83 C.2.7,78 D.2.7,83
[思路点拨]本题涉及数理统计的若干知识.
[正确解答]由图象可知,前4组的公比为3,最大频率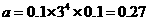 ,设后六组公差为
,设后六组公差为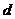 ,则
,则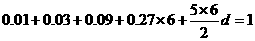 ,解得:
,解得: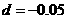 ,
,
后四组公差为-0.05, 所以,视力在4.6到5.0之间的学生数为(0.27+0.22+0.17+0.12)×100=78(人).选A.
[解后反思]本题是一道数理统计图象题,关于统计一般可分为三步,第一步抽样,第二步根据抽样所得结果,画成图形,第三步根据图形,分析结论.本题是统计的第二步,在此类问题中,可画成两种图形,一个是频率分布直方图,另一个是频率分布条形图,两者有很大的不同,前者是以面积表示频数,频率分布条形图是以高度表示频数.
10.已知实数a、b满足等式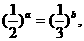 下列五个关系式:
下列五个关系式:
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
见理科卷10.
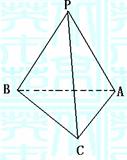
9.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为 ( )
A.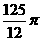 B.
B.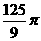 C.
C.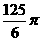 D.
D.
见理科卷9.
8.在△ABC中,设命题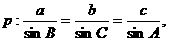 命题q:△ABC是等边三角形,那么命题p是命题q的 ( )
命题q:△ABC是等边三角形,那么命题p是命题q的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
[思路点拨]本题主要考查三角形形状的判断及充要条件.
[正确解答] ,由△ABC是等边三角形,则
,由△ABC是等边三角形,则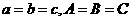 ,显然成立.
,显然成立.
 :由三角形的性质可知:
:由三角形的性质可知: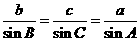 ,又已知,
,又已知,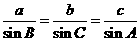
两式相除得: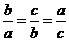 ,令
,令 ,则
,则 ,
,
所以,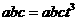 ,得
,得 ,因此
,因此 ,即△ABC是等边三角形.
,即△ABC是等边三角形.
因此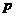 是
是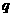 的充分必要条件,选C
的充分必要条件,选C
[解后反思]判断三角形形状,主要根据正弦定理,余弦定理及三角形内角和为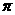 ,化简有两个方向,(1) 角化边,(2)边化角.
,化简有两个方向,(1) 角化边,(2)边化角.
7.将9个(含甲、乙)平均分成三组,甲、乙分在同一组,则不同分组方法的种数为 ( )
A.70 B.140 C.280 D.840
[思路点拨]本题涉及组合的平均分组问题.
[正确解答]要使甲、乙分在同一组,即将剩下的7人分成三组,其中两组有三个人,一组只有一个人,所以要求的概率为 ,选A
,选A
[解后反思]对于平均分组问题,由于各组地位均等,所以平均分成几组,就一定要除以
4.函数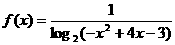 的定义域为 ( )
的定义域为 ( )
A.(1,2)∪(2,3) B.
C.(1,3) D.[1,3]
[思路点拨]本题涉及求函数定义域的若干知识.在本题中,求定义域要注意两个方面(1)因式有分母,注意分母不能为零,(2)因式有对数,要对数有意义.
[正确解答]由题意可知,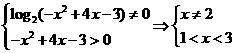 ,选A
,选A
[解后反思]本题是求定义域的一道常规题目, 函数的定义域(或变量的允许取值范围)看似非常简单,然而在解决问题中若不加以注意,常常会误入歧途,导致失误.此外在用函数方法解决实际问题时,必须要注意到函数定义域的取值范围对实际问题的影响.

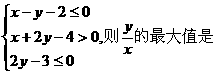 .
.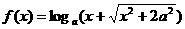 是奇函数,则a=
.
是奇函数,则a=
. 见理科卷13
见理科卷13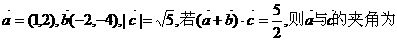 ( )
( ) 为 ( )
为 ( ) B.周期函数,最小正周期为
B.周期函数,最小正周期为 D.非周期函数
D.非周期函数