(13)若正整数m满足 ,则m = 155 .
,则m = 155 .
[解析]∵ ,∴
,∴ ,即
,即 ,
,
∴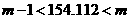 ,即
,即  ,∴
,∴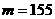 .
.
[点拨]把指数形式化成对数形式.
(14)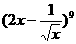 的展开式中,常数项为 672 .(用数字作答)
的展开式中,常数项为 672 .(用数字作答)
[解析]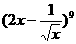 的通项公式为
的通项公式为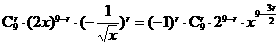 ,令
,令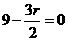 得,
得, ,∴常数项为
,∴常数项为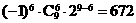
[点拨]熟悉二项式定理的展开式的通项公式.
(15) 的外接圆的圆心为O,两条边上的高的交点为H,
的外接圆的圆心为O,两条边上的高的交点为H,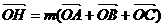 ,则实数
,则实数 .
.
[解析](特例法)设 为一个直角三角形,则O点斜边的中点,H点为直角顶点,这时有
为一个直角三角形,则O点斜边的中点,H点为直角顶点,这时有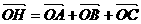 ,∴
,∴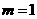 .(但当
.(但当 为正三角形时,m∈R)
为正三角形时,m∈R)
[点拨]由特殊情况去检验一般情况.
(16)在正方体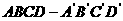 中,过对角线
中,过对角线 的一个平面交
的一个平面交 于E,交
于E,交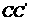 于F,则
于F,则

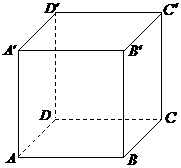 ①四边形
①四边形 一定是平行四边形
一定是平行四边形
②四边形 有可能是正方形
有可能是正方形
③四边形 在底面ABCD内的投影一定是正方形
在底面ABCD内的投影一定是正方形
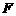

 ④四边形
④四边形 有可能垂直于平面
有可能垂直于平面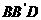
 以上结论正确的为
.(写出所有正确结论的编号)
以上结论正确的为
.(写出所有正确结论的编号)
[解析]①平面 与相对侧面相交,交线互相平行,
与相对侧面相交,交线互相平行,
∴四边形 一定是平行四边形;
一定是平行四边形;
②四边形 若是正方形,则
若是正方形,则 ,又
,又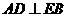 ,
,
∴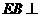 平面
平面 ,产生矛盾;
,产生矛盾;
③四边形 在底面ABCD内的投影是正方形
在底面ABCD内的投影是正方形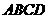 ;
;
④当E、F分别是 、
、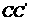 的中点时,
的中点时, ,又
,又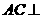 平面
平面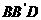 ,
,
∴四边形 有可能垂直于平面
有可能垂直于平面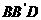 ;
;
[点拨]边观察、边推导.
(1)复数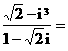 ( )
( )
(A) (B)
(B)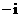 (C)
(C)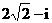 (D)
(D)
[解析]∵ ,故选A.
,故选A.
[点拨]对于复数运算应先观察其特点再计算,会简化运算.
(2)设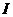 为全集,
为全集,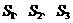 是
是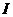 的三个非空子集,且
的三个非空子集,且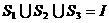 ,则下面论断正确的是( )
,则下面论断正确的是( )
 (A)
(A)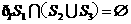 (B)
(B)
(C)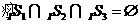 (D)
(D)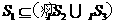
[解析]∵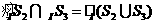 所表示的部分是图中蓝色
所表示的部分是图中蓝色
的部分, 所表示的部分是图中除去
所表示的部分是图中除去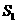 的部分,
的部分,
∴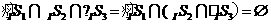 ,故选C.
,故选C.
[点拨]利用韦恩图求解.
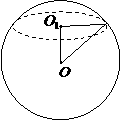
(3)一个与球心距离为1的平面截球所得的圆面面积为 ,则球的表面积为 ( )
,则球的表面积为 ( )
 (A)
(A) (B)
(B) (C)
(C) (D)
(D)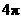
[解析]∵截面圆面积为 ,∴截面圆半径
,∴截面圆半径 ,
,
∴球的半径为 ,
,
∴球的表面积为 ,故选B.
,故选B.
[点拨]找相关的直角三角形.
(4)已知直线 过点
过点 ,当直线
,当直线 与圆
与圆 有两个交点时,其斜率k的取值范围是( )
有两个交点时,其斜率k的取值范围是( )
(A)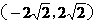 (B)
(B)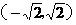
(C)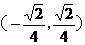 (D)
(D)
将 化为
化为 ,
,
∴该圆的圆心为 ,半径
,半径 ,
,
设直线的方程为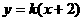 ,即
,即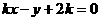 ,设直线
,设直线 到圆心的距离为
到圆心的距离为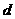 ,则
,则
∵直线 与圆
与圆 有两个交点,∴
有两个交点,∴ ,
,
∴ ,∴
,∴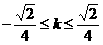 .故选C.
.故选C.
[点拨]利用圆心到直线的距离解直线与圆的位置关系.
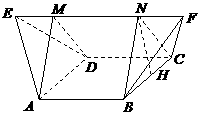 (5)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且
(5)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且 均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
(A) (B)
(B)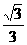
(C)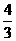 (D)
(D)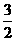
[解析]过A、B两点分别作AM、BN垂直于EF,垂足分别为M、N,连结DM、CN,可证得DM⊥EF、CN⊥EF,多面体ABCDEF分为三部分,多面体的体积V为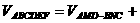
 ,∵
,∵ ,
,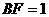 ,∴
,∴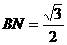 ,作NH垂直于点H,则H为BC的中点,则
,作NH垂直于点H,则H为BC的中点,则 ,∴
,∴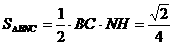 ,∴
,∴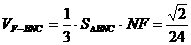 ,
,
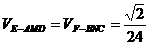 ,
,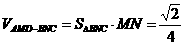 ,∴
,∴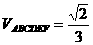 ,故选A.
,故选A.
[点拨]将不规则的多面体分割或补全为规则的几何体进行计算.
(6)已知双曲线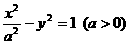 的一条准线与抛物线
的一条准线与抛物线 的准线重合,则该双曲线的离心率为( )
的准线重合,则该双曲线的离心率为( )
(A)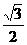 (B)
(B)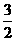 (C)
(C)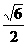 (D)
(D)
[解析]由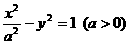 得
得 ,∴
,∴ ,抛物线
,抛物线 的准线为
的准线为 ,因为双曲线
,因为双曲线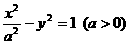 的一条准线与抛物线
的一条准线与抛物线 的准线重合,所以
的准线重合,所以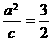 ,解得
,解得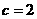 ,所以
,所以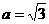 ,所以离心率为
,所以离心率为 ,故选D.
,故选D.
[点拨]熟悉圆锥曲线各准线方程.
(7)当 时,函数
时,函数 的最小值为( )
的最小值为( )
(A)2 (B)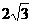 (C)4 (D)
(C)4 (D)
[解析]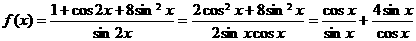
 ,当且仅当
,当且仅当 ,即
,即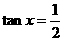 时,取“
时,取“ ”,∵
”,∵ ,∴存在
,∴存在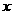 使
使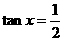 ,这时
,这时 ,故选.
,故选.
[点拨]熟练运用三角函数公式进行化简运算.
(8)设 ,二次函数
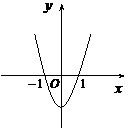
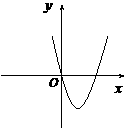
,二次函数 的图像为下列之一
的图像为下列之一
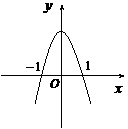

则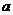 的值为( )
的值为( )
(A)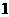 (B)
(B)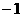 (C)
(C)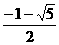 (D)
(D)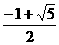
[解析]∵ ,∴图像不能以轴为对称轴,∴一、二两个图不符;第四个图可知,
,∴图像不能以轴为对称轴,∴一、二两个图不符;第四个图可知, ,故其对称轴为
,故其对称轴为 ,所以也不符合;只有第三个图可以,由图象过原点,得
,所以也不符合;只有第三个图可以,由图象过原点,得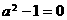 ,开口向下,所以
,开口向下,所以 ,故选B.
,故选B.
[点拨]熟悉二次函数图象的特点,分析对称轴、与轴的交点等形与数的关系.
(9)设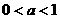 ,函数
,函数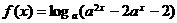 ,则使
,则使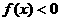 的
的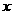 的取值范围是( )
的取值范围是( )
(A)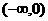 (B)
(B)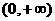 (C)
(C) (D)
(D)
[解析]∵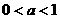 ,
,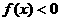 ,∴
,∴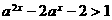 ,解得
,解得  或
或 (舍去),
(舍去),
∴ ,故选C.
,故选C.
[点拨]熟悉对数的性质.
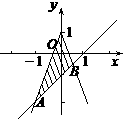 (10)在坐标平面上,不等式组
(10)在坐标平面上,不等式组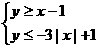 所表示的平面区域的面积为( )
所表示的平面区域的面积为( )
(A) (B)
(B)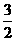 (C)
(C) (D)2
(D)2
[解析]原不等式化为 或
或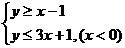 ,
,
所表示的平面区域如右图所示,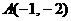 ,
, , ∴
, ∴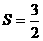 ,故选B.
,故选B.
[点拨]分类讨论,通过画出区域,计算面积.
(11)在 中,已知
中,已知 ,给出以下四个论断:
,给出以下四个论断:
① ②
②
③ ④
④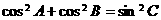
其中正确的是( )
(A)①③ (B)②④ (C)①④ (D)②③
[解析]∵ ,
,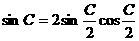 ,
,
∴ ,∴
,∴ ,
,
∵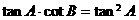 ,∴①不一定成立,
,∴①不一定成立,
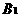 ∵
∵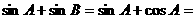
 ,∴
,∴ ,∴②成立,
,∴②成立,


 ∵
∵ ,∴③不一定成立,
,∴③不一定成立,
 ∵
∵ ,∴④成立,故选B.
,∴④成立,故选B.



 [点拨]考查三角公式的灵活运用.
[点拨]考查三角公式的灵活运用.
(12)过三棱柱任意两个顶点的直线共15条,其中异面直线有( )
(A)18对 (B)24对 (C)30对 (D)36对
 [解析]解法一:(直接法)
[解析]解法一:(直接法)
①与上底面的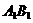 、
、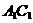 、
、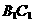 成异面直线的有15对;
成异面直线的有15对;
②与下底面的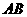 、
、 、
、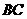 成异面直线的有9对(除去与上底面的);
成异面直线的有9对(除去与上底面的);
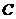
 ③与侧棱
③与侧棱 、
、 、
、 成异面直线的有6对(除去与上下底面的);
成异面直线的有6对(除去与上下底面的);
④侧面对角线之间成异面直线的有6对;
所以异面直线总共有36对.
解法二:(间接法)
①共一顶点的共面直线有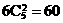 对;
对;
②侧面互相平行的直线有6对;
③侧面的对角线有3对共面;
所以异面直线总共有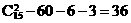 对.
对.
[点拨]解排列组合题的关键是分好类.
第Ⅱ卷
21.(本小题满分12分)
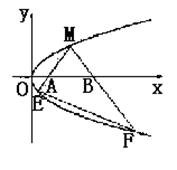 如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程.
[思路点拨]本题涉及抛物线与直线相交的有关知识.
[正确解答](1)设M(y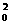 ,y0),直线ME的斜率为k(l>0)
,y0),直线ME的斜率为k(l>0)
则直线MF的斜率为-k,
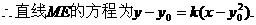
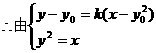 消
消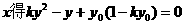

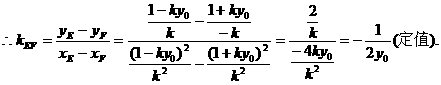
所以直线EF的斜率为定值
(2)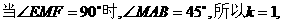
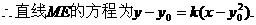
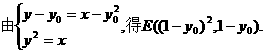
同理可得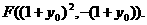
设重心G(x, y),则有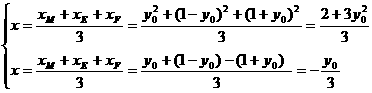
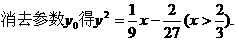
[解后反思]这是一道重要的数学问题,它属于解析几何范畴,几乎是高考数学每年的必考内容之一,此类问题一定要”大胆假设,细心求解”,根据题目要求先将题目所涉及的未知量都可以设出来,然后根据题目把所有的条件都变成等式,一定可以求出来,当然求的过程中,采取适当的小技巧,例如化简或适当分类讨论,可以大为简化过程,而且会尽量多多得分,同时这一类题目也需要很强的计算能力.
20.(本小题满分12分)
如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
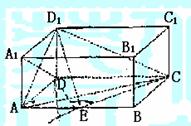 (1)证明:D1E⊥A1D;
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为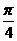 .
.
见理科卷20.
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.
[思路点拨]本题涉及随机事件的有关概率.
[正确解答]设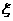 表示游戏终止时掷硬币的次数,
表示游戏终止时掷硬币的次数,
设正面出现的次数为m,反面出现的次数为n,则 ,可得:
,可得:
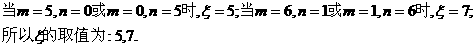
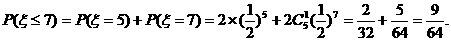
[解后反思]这是一道比较复杂的概率题目,首先我们应理解随机变量及其概率分布的概念,掌握分布函数F(x)= P{X≤x}的概念及性质;才能会计算与随机变量相关的事件的概率.同时我们在解决的过程中,也适当对此类解题的流程也要有一个清晰的了解,这样才能保证此类题目得高分和全分.
18.(本小题满分12分)
已知向量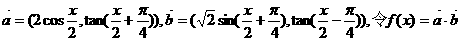 .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
[思路点拨]本题主要考查向量与三角函数的综合题,正确求出f(x)是解该题的关键.
[正确解答]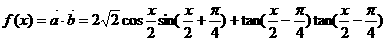
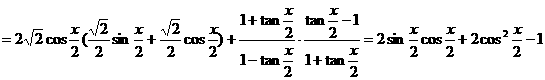
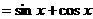 =
=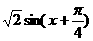 .
.
所以 ,最小正周期为
,最小正周期为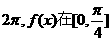 上单调增加,
上单调增加, 上单调减少.
上单调减少.
[解后反思]这是一道向量与三角函数的综合题,向量虽然是近年高中数学出现的新知识,但向量知识却很重要.因为向量是近代数学中重要和基本的数学概念之一,它是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景.在学习过程中,同学将会了解向量丰富的实际背景,逐渐理解平面向量及其运算的意义,一定能要用向量语言和方法表述和解决数学和物理中的一些问题,发展数学运算能力和解决数学实际问题的能力.
17.(本小题满分12分)
已知函数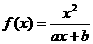 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;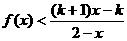 .
.
见理科卷17.
16.以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,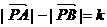 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若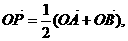 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程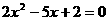 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
见理科卷16.
15.如图,在三棱锥P-ABC中,PA=PB=PC=BC,
且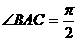 ,则PA与底面ABC所成角为
,则PA与底面ABC所成角为
.
[思路点拨]本题主要考查直线与平面所成的角的求法,关键是
确定点P在底面的射影O的位置.
[正确解答]过P作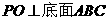 ,交底面于O,连结AO并延长交BC于D,连结PD,则PD、AD均垂直于BC,所以AB=AC,PA与底面ABC所成角为
,交底面于O,连结AO并延长交BC于D,连结PD,则PD、AD均垂直于BC,所以AB=AC,PA与底面ABC所成角为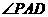 ,
,
设AC=1,则PA=PB=PC=BC=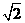 ,
,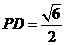 ,
,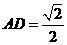 ,
,
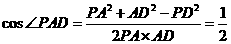 ,所以
,所以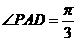 .
.
[解后反思]熟练掌握三角形的“四心”是快速解该题的关键.外心:三角形三条中垂线的交点,性质外心到三角顶点距离相等,内心:内角平分线的交点,性质是内心到三边距离相等,垂心:三条高线的交点,重心:三条中线的交点,另外记住一些结论也是大有裨益的,比如在三棱锥P-ABC中(1)若P到三个顶点的距离相等,则P在底面的射影是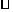 ABC的外心,(2)若P到三边的距离相等,则P在底面的射影是
ABC的外心,(2)若P到三边的距离相等,则P在底面的射影是 的内心,(3)若
的内心,(3)若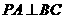
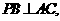 则
则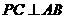 且P在底面的射影是
且P在底面的射影是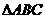 的垂心.
的垂心.

 .
.