5、函数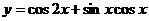 的最小正周期T=__________.
的最小正周期T=__________.
[思路点拨]本题考查二倍角公式等基础知识和变换能力,角的差异(由异角化同角)在同角的条件下,利用三角恒等式化成正弦函数,就可求出最小正周期.
[正确解答] ,得最小正周期为
,得最小正周期为
[解后反思]三角函数的变换要注意变换的方向,消除差异,达到转化.
3、若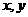 满足条件
满足条件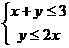 ,则
,则 的最大值是__________.
的最大值是__________.
[思路点拨]本题考查线性规划的基础知识,画出可行域,寻求目标函数的最大值.
[正确解答]求 的最大值,即求
的最大值,即求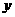 轴上的截距最大值,由图可知,过点(1,2)时有最大值,为11
轴上的截距最大值,由图可知,过点(1,2)时有最大值,为11
[解后反思]线性规划是直线方程的应用,是新增的教学内容.要了解线性不等式表示的平面区域,了解线性规划的定义,会求在线性约束条件下的目标函数的最优解.
(17)(本小题满分12分)
已知向量 和
和 ,且
,且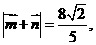 求
求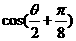 的值.
的值.
(18)(本小题满分12分)
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用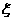 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中原有白球的个数;
(II)求随机变量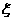 的概率分布;
的概率分布;
(III)求甲取到白球的概率.
(19)(本小题满分12分)
已知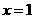 是函数
是函数 的一个极值点,其中
的一个极值点,其中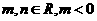 ,
,
(I)求 与
与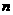 的关系式;
的关系式;
(II)求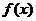 的单调区间;
的单调区间;
(III)当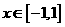 时,函数
时,函数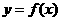 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
(20)(本小题满分12分)
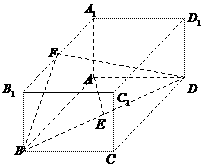 如图,已知长方体
如图,已知长方体
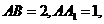 直线
直线 与平面
与平面 所成的角为
所成的角为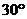 ,
,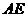 垂直
垂直 于
于 ,
,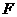 为
为 的中点.
的中点.
(I)求异面直线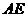 与
与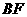 所成的角;
所成的角;
(II)求平面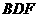 与平面
与平面 所成的二面角;
所成的二面角;
(III)求点 到平面
到平面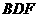 的距离.
的距离.
(21)(本小题满分12分)
已知数列 的首项
的首项 前
前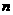 项和为
项和为 ,且
,且
(I)证明数列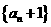 是等比数列;
是等比数列;
(II)令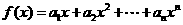 ,求函数
,求函数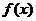 在点
在点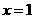 处的导数
处的导数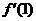 并比较
并比较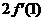 与
与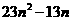 的大小.
的大小.
(22)(本小题满分14分)
已知动圆过定点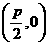 ,且与直线
,且与直线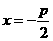 相切,其中
相切,其中 .
.
(I)求动圆圆心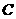 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹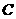 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线 和
和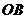 的倾斜角分别为
的倾斜角分别为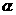 和
和 ,当
,当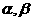 变化且
变化且 为定值
为定值 时,证明直线
时,证明直线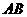 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
(13) .
.
(14)设双曲线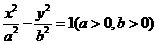 的右焦点为
的右焦点为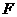 ,右准线
,右准线 与两条渐近线交于P、
与两条渐近线交于P、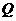 两点,如果
两点,如果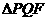 是直角三角形,则双曲线的离心率
是直角三角形,则双曲线的离心率 .
.
(15)设 、
、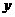 满足约束条件
满足约束条件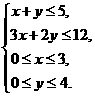 则使得目标函数
则使得目标函数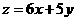 的最大的点
的最大的点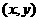 是____________
是____________
(16)已知 是不同的直线,
是不同的直线,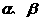 是不重合的平面,给出下列命题:①若
是不重合的平面,给出下列命题:①若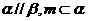 ,
, 则
则 ;②若
;②若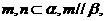 则
则 ③若
③若 ,则
,则 ④
④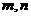 是两条异面直线,若
是两条异面直线,若 ,则
,则
上面的命题中,真命题的序号是 (写出所有真命题的序号)
(写出所有真命题的序号)
(1)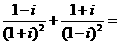
(A)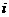 (B)
(B)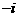 (C)1 (D)
(C)1 (D)
(2)函数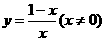 的反函数图像大致是
的反函数图像大致是

(A) (B) (C) (D)
(3)已知函数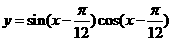 ,则下列判断正确的是
,则下列判断正确的是
(A)此函数的最小周期为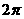 ,其图像的一个对称中心是
,其图像的一个对称中心是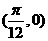
(B)此函数的最小周期为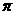 ,其图像的一个对称中心是
,其图像的一个对称中心是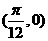
(C)此函数的最小周期为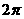 ,其图像的一个对称中心是
,其图像的一个对称中心是
(D)此函数的最小周期为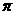 ,其图像的一个对称中心是
,其图像的一个对称中心是
(4)下列函数既是奇函数,又在区间 上单调递减的是
上单调递减的是
(A)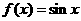 (B)
(B)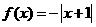 (C)
(C)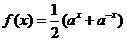 (D)
(D)
(5)如果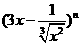 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中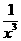 的系数是
的系数是
(A)7
(B) (C)21
(D)
(C)21
(D)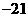
(6)函数 ,若
,若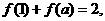 则
则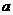 的所有可能值为
的所有可能值为
(A)1
(B)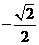 (C)
(C) (D)
(D)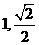
(7)已知向量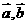 ,且
,且 ,
,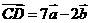 ,则一定共线的三点是
,则一定共线的三点是
(A)A、B、D (B)A、B、C (C)B、C、D (D)A、C、D
(8)设地球的半径为 ,若甲地位于北纬
,若甲地位于北纬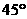 东经
东经 ,乙地位于南纬
,乙地位于南纬 东经
东经 ,则甲、乙两地的球面距离为
,则甲、乙两地的球面距离为
(A)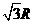 (B)
(B)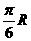 (C)
(C)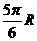 (D)
(D)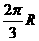
(9)10张奖券中只有3张有奖,5个人购买,至少有1人中奖的概率是
(A) (B)
(B)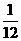 (C)
(C)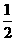 (D)
(D)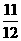
(10)设集合A、B是全集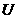 的两个子集,则
的两个子集,则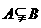 是
是 的
的
(A)充分不必要条件(B)必要不充分条件(C)冲要条件(D)既不充分也不必要条件
(11)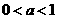 ,下列不等式一定成立的是
,下列不等式一定成立的是
(A)
(B)
(C)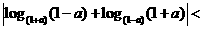

(D)

(12)设直线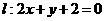 关于原点对称的直线为
关于原点对称的直线为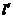 ,若
,若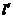 与椭圆
与椭圆 的交点为A、B、,点
的交点为A、B、,点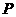 为椭圆上的动点,则使
为椭圆上的动点,则使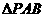 的面积为
的面积为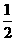 的点
的点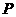 的个数为
的个数为
(A)1 (B)2 (C)3 (D)4
第II卷(共90分)
22. (本小题满分14分)
设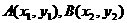 两点在抛物线
两点在抛物线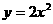 上,
上,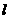 是AB的垂直平分线,
是AB的垂直平分线,
(Ⅰ)当且仅当 取何值时,直线
取何值时,直线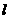 经过抛物线的焦点F?证明你的结论;
经过抛物线的焦点F?证明你的结论;
(Ⅱ)当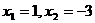 时,求直线
时,求直线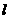 的方程.
的方程.
21. (本小题满分12分)
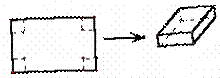
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小
正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最
大?最大容积是多少?
……

 中,若定点
中,若定点 与动点
与动点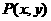 满足
满足 ,则点P的轨迹方程是__________.
,则点P的轨迹方程是__________. 的解是__________.
的解是__________.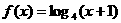 的反函数
的反函数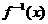 =__________.
=__________.