15.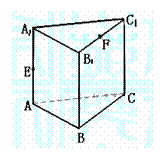 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,
AB=BC=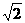 ,BB1=2,
,BB1=2,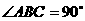 ,
,
E、F分别为AA1、C1B1的中点,沿棱柱的表面从E
到F两点的最短路径的长度为 .
[思路点拨]本题主要考查空间距离转化为平面距离.
[正确解答]分别延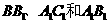 将E、F展开到同一平面内,则易得:
将E、F展开到同一平面内,则易得: ,
,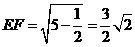 ,或
,或
比较可得,最小值为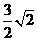 .
.
[解后反思]将平面图形空间化也是立体几何的另一种问题形式,在做立体几何中,许多问题都是空间图形进行平面化,努力将一个个空间图形,通过所学的几何知识,转化成平面图形,最后使用平面几何的若干知识解决,而本题却反其道而行之,所以在做法上就不能和上述的方法相同,但在本质上有许多相通之处,在这类题目中,尽量找出两者图形过程中的联系之处,哪些量变啦,哪些量没有变,然后解决起来,就会顺手多啦.
14. 设实数x,
y满足
设实数x,
y满足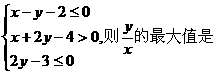 .
.
[思路点拨]本题主要考查线性规划问题,由线性约束条件画出可行域,然后求出目标函数的最值.
[正确解答]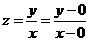 表示两点(0,0),A(x,y)的斜率
表示两点(0,0),A(x,y)的斜率
[解后反思]解题的关键是理解目标函数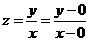 的几何意义,类似的你知道
的几何意义,类似的你知道 的几何意义吗?
的几何意义吗?
13.若函数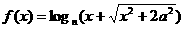 是奇函数,则a=
.
是奇函数,则a=
.
[思路点拨]本题主要考查函数的奇偶性,由函数的奇偶性的定义可求得.
[正确解答]
解法1:由题意可知, ,即
,即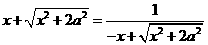 ,
,
因此 ,
,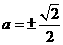 .
.
解法2:函数的定义域为R,又f(x)为奇函数,故其图象必过原点即f(0)=0,所以 ,得
,得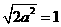 即
即 推出答案
推出答案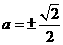
[解后反思]对数学概念及定理公式的深刻理解是解数学问题的关健,讨论函数的奇偶性,其前提条件是函数的定义域必须关于原点对称.
若函数f(x)为奇函数 的图象关于原点对称.
的图象关于原点对称.
若函数f(x)为偶函数 的图象关于y轴对称.
的图象关于y轴对称.
12.将1,2,…,9这9个数平均分成三组,则每组的三个数都成等差数列的概率为( )
A. B.
B. C.
C. D.
D.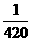
[思路点拨]本题主要考查平均分组问题及概率问题.
[正确解答]将1,22-------9平均分成三组的数目为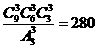 ,又每组的三个数成等差数列,种数为了4,所以答案为B
,又每组的三个数成等差数列,种数为了4,所以答案为B
[解后反思]这是一道概率题,属于等可能事件,在求的过程中,先求出不加条件限制的所有可能性a,然后再根据条件,求出满足题目要求的可能种数b,最后要求的概率就是 .
.
11.在△OAB中,O为坐标原点, ,则△OAB的面积达到最大值时,
,则△OAB的面积达到最大值时, ( )
( )
A. B.
B.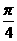 C.
C. D.
D.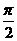
[思路点拨]运用图形,根据图形表示 的面积,将实际问题转化成数学问题.
的面积,将实际问题转化成数学问题.
[正确解答]


当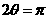 即
即 时,面积最大.
时,面积最大.
[解后反思]运用三角函数解决相应的实际问题,首先应根据题目的要求将面积的表达式写出来,然后在表达式中,根据自变量的取值范围,最终求出答案,所要注意的是,解决此类问题时不能仅凭函数的表达式,应考虑实际情况,例如,在函数的自变量中,可以取负数,而如果在实际题目中,自变量表示的是天数,那么这相自变量必须为正数,且为整数等等.
10.已知实数a,
b满足等式 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
[思路点拨]本题涉及指数函数的若干知识.
[正确解答] 均大于零时,要满足等式,必有
均大于零时,要满足等式,必有 ;
; 均小于零时,要满足等式,必有
均小于零时,要满足等式,必有 ;
; 时,显然等式成立.因此不可能成立的关系式为③④,选B
时,显然等式成立.因此不可能成立的关系式为③④,选B
[解后反思]根据函数图形来解客观题,快速而且准确,这就要求对函数的图形要相当了解.
9.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为 ( )
A.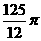 B.
B.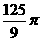 C.
C. D.
D.
[思路点拨]本题主要考查图形的翻折问题,利用球心到球面的距离均相等,找出球心是解本题的关健.
[正确解答]连接矩形ABCD的对角线AC、BD交于O,则AO=BO=CO=DO,则O为四面体ABCD的外接球的圆心,因此四面体ABCD的外接球的半径为 ,体积为
,体积为 .选C.
.选C.
[解后反思]对于图形的翻折问题,关健是利用翻折前后的不变量,另外,球和正方体,长方体,三棱锥的组合问题,应引起高度重视,而且有些问题也可以通过补形法转化成球内接正方体或内接长方体问题.
8.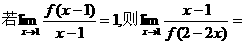 ( )
( )
A.-1 B.1 C.- D.
D.
[思路点拨]本题主要是考查函数极限法则的运用,涉及函数在某一点的极限的有关知识.
[正确解答]令 ,则
,则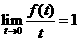 ,令
,令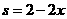 ,则
,则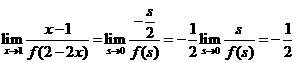 .选C.
.选C.
[解后反思]本题首先利用整体代换的方法,简化极限运算中式子,然后使用配凑法,将最值式子进行简化,再将简化后的条件代入因式,得出解.在做这一类题目时,先适当的将条件化简是解决的关健.
7. 已知函数
已知函数
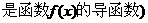 ,下面四个图象中
,下面四个图象中
 的图象大致是 ( )
的图象大致是 ( )
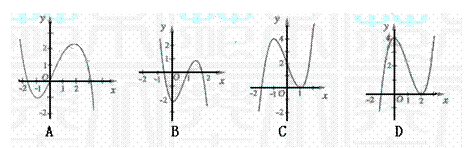
[思路点拨]本题考查导函数的图象及其性质,由图象得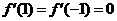 ,从而导出
,从而导出 是函数f(x)极值点是解本题的关健.
是函数f(x)极值点是解本题的关健.
[正确解答]由图象知,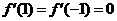 ,所以
,所以 是函数
是函数 的极值点,又因为在
的极值点,又因为在 上,
上, ,在
,在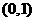 上,
上, ,因此在
,因此在 上,
上, 单调递减,故选C.
单调递减,故选C.
[解后反思]要注意,若 是函数y=f(x)的极值点,则有
是函数y=f(x)的极值点,则有 ,但是若
,但是若 ,则是
,则是 不一定是函数y=f(x)极值点,所以要判断一个点是否为极值点,还要检验点
不一定是函数y=f(x)极值点,所以要判断一个点是否为极值点,还要检验点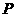 的两侧的单调性是否不同.
的两侧的单调性是否不同.
6.已知向量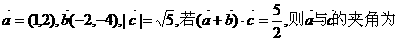 ( )
( )
A.30° B.60°
C.120° D.150°
[思路点拨]本题考查平面向量的运算及向量的夹角公式.
[正确解答]设 ,则
,则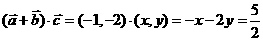 ,又
,又
 ,所以
,所以 ,得
,得 ,
,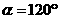 ,
,
选C.
[解后反思]设 的夹角为
的夹角为 ,则
,则 ,(1)当
,(1)当 为锐角,有
为锐角,有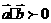 且
且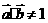 (2) 当
(2) 当 为钝角,有
为钝角,有 且
且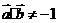 (3)当
(3)当 ,
, 共线且方向相同.(4)当
共线且方向相同.(4)当 时,
时,  .
.

