15、条件甲:“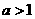 ”是条件乙:“
”是条件乙:“ ”的( )
”的( )
A.既不充分也不必要条件B.充要条件 C.充分不必要条件 D.必要不充分条件
[思路点拨]本题考查了充要条件的定义及其判定只要判断甲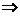 乙和乙
乙和乙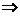 甲的真假性,利用充要条件将条件乙进行化简是解决这类问题的关键.
甲的真假性,利用充要条件将条件乙进行化简是解决这类问题的关键.
[正确解答]解法1:甲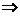 乙:
乙: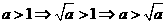 ,
,
乙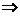 甲:
甲: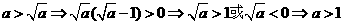
因此是充要条件,选B
解法2:∵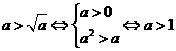 ,∴选B
,∴选B
[解后反思]对命题的充要条件、必要条件可以从三个方面理解:①定义法,②等价法,即利用 与
与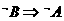 ,
, 与
与 的等价关系,对于条件或结论是否定式的命题一般采用等价法,③利用集合间的包含关系判断:若
的等价关系,对于条件或结论是否定式的命题一般采用等价法,③利用集合间的包含关系判断:若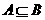 则A是B的充分条件或B是A必要条件;若
则A是B的充分条件或B是A必要条件;若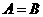 则A是B的充要条件,另外,对于确定条件的不充分性或不必要性往往用构造反例的方法来说明.
则A是B的充要条件,另外,对于确定条件的不充分性或不必要性往往用构造反例的方法来说明.
12、有两个相同的直三棱柱,高为 ,底面三角形的三边长分别为
,底面三角形的三边长分别为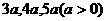 .用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则
.用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则 的取值范围是__________.
的取值范围是__________.
见理11
9、直线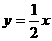 关于直线
关于直线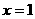 对称的直线方程是__________.
对称的直线方程是__________.
[思路点拨]本题考查一条直线关于已知直线对称的直线方程,可取两个特殊点求出关于直线的对称点的坐标,再由两点式求出直线方程即可.
[正确解答]直线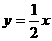 上的点(0,0)关于
上的点(0,0)关于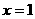 对称的点是(2,0),且所求方程的斜率为-
对称的点是(2,0),且所求方程的斜率为- ,因此,直线
,因此,直线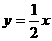 关于直线
关于直线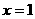 对称的直线方程是:
对称的直线方程是:
 ,整理后得
,整理后得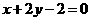 .
.
解法2设所求直线上任意点 关于直线x=1对称点为
关于直线x=1对称点为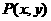 则
则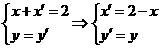 ∵
∵ ∴
∴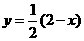 即x+2y-2=0
即x+2y-2=0
[解后反思]解法2是通法,详见理22.
8、某班有50名学生,其中15人选修A课程,另外35人选修B课程.从班级中任选两名学生,他们是选修不同课程的学生的概率是__________.(结果用分数表示)
见理8
7、若椭圆长轴长与短轴长之比为2,它的一个焦点是 ,则椭圆的标准方程是__________.
,则椭圆的标准方程是__________.
[思路点拨]本题考查椭圆的基础知识,数形的等价转换是解决此类型的关键.
[正确解答]由题意可知, ,
,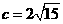 ,又
,又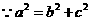 ,解得
,解得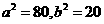 ,
,
所求椭圆的标准方程为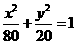 .
.
[解后反思]在求椭圆方程和研究性质时,要深刻理解确定椭圆的形状及大小的主要特征数,如a、b、c、p、e的几何意义及它们的关系式,熟练运用这些公式解决有关问题..
6、若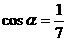 ,
,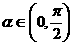 ,则
,则 =__________.
=__________.
[思路点拨本题考查两个角和的余弦的求法.熟记公式结构,根据条件求出运用公式必需值,再考虑三角函数的符号.
[正确解答]
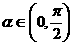 ,
,
 ,
,
 .
.
[解后反思]在三角函数的公式运用过程中取决于满足运用公式的条件,已知三角函数值求同角的其它三角函数值时必须注意符号,否则就无所谓解决三角函数问题.

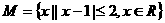 ,
,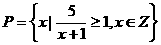 ,则
,则 等于( )
等于( )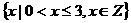 B.
B.
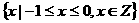 D.
D.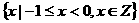
 ,则该函数在
,则该函数在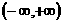 上是( )
上是( )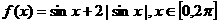 的图象与直线
的图象与直线 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则 的取值范围是__________.
的取值范围是__________. 中,若
中,若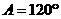 ,AB=5,BC=7,则AC=__________.
,AB=5,BC=7,则AC=__________.