(13)若正整数m满足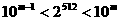 ,则m = 。
,则m = 。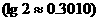
解:∵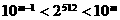 ,∴
,∴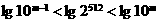 ,即
,即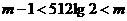 ,
,
∴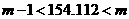 ,即
,即 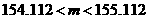 ,∴
,∴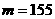 .
.
(14)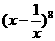 的展开式中,常数项为
。(用数字作答
的展开式中,常数项为
。(用数字作答
解: 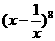 的通项公式为
的通项公式为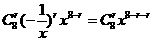 ,令8-2r=0,得r=4,∴常数项为70.
,令8-2r=0,得r=4,∴常数项为70.
(15)从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有 种。
解:用剔除法.: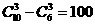 ,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。
,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。
(16)在正方形 中,过对角线
中,过对角线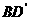 的一个平面交
的一个平面交 于E,交
于E,交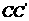 于F,
于F,
①
四边形 一定是平行四边形
一定是平行四边形
②
四边形 有可能是正方形
有可能是正方形
③
四边形 在底面ABCD内的投影一定是正方形
在底面ABCD内的投影一定是正方形
④
四边形 有可能垂直于平面
有可能垂直于平面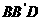
以上结论正确的为 。(写出所有正确结论的编号)
 解:①平面
解:①平面 与相对侧面相交,交线互相平行,
与相对侧面相交,交线互相平行,
∴四边形 一定是平行四边形;
一定是平行四边形;
②四边形 若是正方形,则
若是正方形,则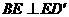 ,又
,又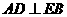 ,
,
∴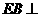 平面
平面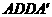 ,产生矛盾;
,产生矛盾;
③四边形 在底面ABCD内的投影是正方形
在底面ABCD内的投影是正方形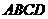 ;
;
④当E、F分别是 、
、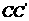 的中点时,
的中点时,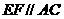 ,又
,又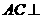 平面
平面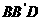 ,
,
∴四边形 有可能垂直于平面,∴填①③④.
有可能垂直于平面,∴填①③④.
- 答案

