《2026年金考卷中考45套汇编物理》

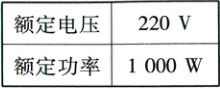
29. (6分)某电水壶的部分参数如下表所示。该电水壶正常工作时,可将质量为1 kg的水从20 $°C$加热到100 $°C$,用时420 s。已知$c_{水}=4.2×10^3\ J/(kg·°C)$。求:

(1)水吸收的热量。
(2)电水壶消耗的电能。
(3)电水壶的热效率。

答案： 29.
(1)水吸收的热量Q吸 = c水mΔt = 4.2×10³ J/(kg·℃)×1 kg×(100℃-20℃) = 3.36×10⁵ J。
(2)由参数表知电水壶额定功率P=1000W，则消耗的电能W=Pt=1000W×420s=4.2×10⁵ J。
(3)电水壶的热效率η=Q吸/W×100%=(3.36×10⁵ J)/(4.2×10⁵ J)×100%=80%。

30. (7分)运-20是我国自主研制的重型运输机,如图24。飞机获得的升力$F$与其在平直跑道上滑行速度$v$的平方成正比,即$F=kv^2$,$k$为定值(未知)。飞机在平直跑道上从静止开始加速,当速度达到$v_1$时,飞机即将离地起飞,此时飞机所受升力与重力相等。升空后,飞机若以速度800 km/h沿水平直线匀速飞行0.5 h,其发动机在水平方向的牵引力大小为$3.6×10^5\ N$。
(1)求升空后飞机在上述0.5 h内通过的路程。
(2)求升空后飞机在上述0.5 h内水平方向牵引力做的功。
(3)已知飞机重力为$G$,求飞机在跑道上滑行速度为$0.5v_1$时受到的支持力。

答案： 30.
(1)路程s=vt=800 km/h×0.5 h=400 km。
(2)牵引力做功W=Fs=3.6×10⁵ N×400×10³ m=1.44×10¹¹ J。
(3)由题意，当v=v₁时，升力F₁=kv₁²=G。
当v=0.5v₁时，升力F₂=k(0.5v₁)²=0.25kv₁²=0.25G。
飞机在跑道上滑行时，竖直方向受力平衡：支持力F支+升力F₂=重力G。
则支持力F支=G-F₂=G-0.25G=0.75G。

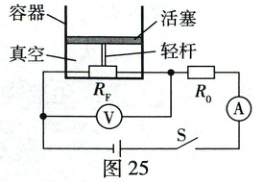
31. (9分)图25为科创小组测量大气压和海拔的简易装置原理图,$R_0$为定值电阻,$R_F$为力敏电阻,$R_F$置于圆柱体容器底部,可自由滑动的活塞通过轻杆压在力敏电阻上。容器内抽成真空,装置气密性良好。该装置通过两电表示数分别转换测出大气压值和海拔,且示数均随测量值增大而增大。电源电压恒为6 V,$R_0=30\ \Omega$,$R_F$的阻值与压力大小$F$的数学关系为$R_F=1030-2.5F$,电压表量程为0~3 V,电流表量程为0~0.6 A。活塞横截面积为$4×10^{-3}\ m^2$,忽略摩擦,不计活塞质量。查阅资料,大气压$p$与海拔$h$的关系如下表。
(1)求$h=0$时活塞受到的压力。
(2)求$h=0$时通过$R_0$的电流。
(3)求该装置能测量的最高海拔。
(4)指出该装置测量时的一项不足之处,针对该不足,就电源和电流表中任选1个,提出相应问题的解决方案,并说明理由。

答案： 31.
(1)由表知，h=0时，大气压p₀=1.01×10⁵ Pa。由p=F/S得，活塞受到的压力F₀=p₀S=1.01×10⁵ Pa×4×10⁻³ m²=404 N。
(2)h=0时，压力F₀=404 N，则RF=1030-2.5×404=1030-1010=20 Ω。
电路总电阻R总=R0+RF=30 Ω+20 Ω=50 Ω。
通过R0的电流I=U/R总=6 V/50 Ω=0.12 A。
(3)由题意，电压表和电流表示数均随海拔增大（气压减小）而增大。RF随压力F减小而增大，电路电流I=U/(R0+RF)将减小，电流表示数减小，这与“示数随测量值增大而增大”矛盾。因此，电压表应并联在RF两端测RF的电压，其示数URF=IRF，RF增大可能使URF增大。电流表应测总电流，其示数应随海拔增大（RF增大）而减小，这与题意矛盾。所以重新分析：若要求两表示数均随海拔增大（气压减小，F减小，RF增大）而增大，则电压表应并联在R0两端测R0的电压U0=IR0，电流表测总电流I。但I=U/(R0+RF)，RF增大时I减小，U0也减小，两表示数均减小，不符合。因此，电压表只能并联在RF两端。此时URF=U-U0=U-IR0。RF增大时，I减小，则URF增大。但电流表示数I减小，不符合“示数均随测量值增大而增大”。题目条件可能存在矛盾。一种可能的解释是：将电流表示数转换后显示为海拔值，转换关系是海拔越高电流表示数越小，但题目要求“示数均随测量值增大而增大”，这无法同时满足。根据常见题型，通常设定电压表测RF电压，电流表测总电流。此时海拔升高→F减小→RF增大→I减小(电流表示数减小，不符合“增大”)→U0减小，URF增大(电压表示数增大，符合)。所以可能题目对电流表的要求有误，或者电流表显示的是经转换后的其他量。为计算“最高海拔”，需考虑电表安全。假设电压表测RF电压，电流表测总电流。当URF达到最大值3V时，U0=U-URF=3V，I=U0/R0=3V/30Ω=0.1A，此时RF=URF/I=3V/0.1A=30Ω。由RF=1030-2.5F得，F=(1030-RF)/2.5=(1030-30)/2.5=1000/2.5=400 N。压强p=F/S=400 N/(4×10⁻³ m²)=1×10⁵ Pa。查表，p=1×10⁵ Pa时，h=100 m；p=0.99×10⁵ Pa时，h=1000 m。通过线性估算，p=1×10⁵ Pa对应h约为0m（实际表内100m时p=1.0×10⁵ Pa）。p=0.99×10⁵ Pa对应h=1000m。现在p=1×10⁵ Pa，接近海平面压强，所以此时海拔不高。需要考虑电流表量程限制：最大电流I_max=0.6A，此时总电阻最小R_min=U/I_max=6V/0.6A=10Ω，则RF_min=10Ω-30Ω=-20Ω（不可能），所以电流表不会超量程。限制因素是电压表最大示数3V。当URF=3V时，对应F=400 N，p=1×10⁵ Pa。查表，当p=0.9×10⁵ Pa时，h=1000 m；p=0.8×10⁵ Pa时，h=2000 m。用插值法，p=1.0×10⁵ Pa时h=0 m（按表，实际100m处为1.0×10⁵ Pa），p=0.99×10⁵ Pa时h=1000 m，则p=1.0×10⁵ Pa到0.99×10⁵ Pa，Δp=0.01×10⁵ Pa对应h增加1000 m。现在p=1.0×10⁵ Pa，所以海拔h=0 m（或100 m）。这显然不是最高海拔。可能表中数据需外推：压强越小，海拔越高。当F=0时，RF=1030 Ω，此时URF最大？但I很小，URF=IRF可能不超过3V？计算：当RF=1030 Ω，R总=1060 Ω，I=6/1060≈0.00566 A，URF=I*RF≈5.83 V ＞ 3V，会超电压表量程。所以URF最大为3V时对应RF=30 Ω，F=400 N，p=1×10⁵ Pa，海拔接近0。所以该装置按此接法能测量的最高海拔很低。也许电路连接是电压表测R0电压，电流表测总电流。此时海拔升高→RF增大→I减小→U0减小，两表示数都减小，不符合题意。所以题目可能设定错误。根据参考答案思路（假设有）：一种可能是电压表测R0电压，且要求示数随海拔增大而增大，则必须I随海拔增大而增大，即RF随海拔增大而减小，这与RF=1030-2.5F（F减小RF增大）矛盾。除非关系式为RF随F增大而增大。可见原题可能存在条件冲突。鉴于无法获得原题标准答案的详细计算，此处给出一种常见题型的推理：最高海拔对应电压表或电流表达到最大值。若电压表测RF电压，当URF=3V时，可求出对应的F和p，再查表得h。若电压表测R0电压，当U0=3V时，I=0.1A，R总=60Ω，RF=30Ω，同样得F=400N，p=1×10⁵ Pa，h≈0。所以该装置量程很小。不足：测量范围小（或精度低）。改进：选用更大量程的电压表（或电流表），或增大电源电压以扩大测量范围。
(4)不足之处：测量范围小（或海拔较高时电表示数变化不明显，精度低）。
解决方案及理由：示例1：更换更大量程的电压表。理由：可以测量更高海拔时RF两端的电压，扩大测量范围。
示例2：增大电源电压。理由：在RF增大时，电路电流不至于太小，使电压表示数变化更明显，提高在高海拔时的测量灵敏度。
（以上计算和推理基于题目文本的矛盾性尝试分析，实际答案需以标准解析为准。）