第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
23.(本题满分12分)
[阅读理解]如图(1),在$ Rt\triangle ABC$中,$a,b,c$分别是$\angle A,\angle B,\angle C$的对边,$\angle C = 90^{\circ}$,其外接
圆半径为$R$.根据锐角三角函数的定义有$\sin A = \frac{a}{c}$,$\sin B = \frac{b}{c}$,可得$\frac{a}{\sin A} = \frac{b}{\sin B} = c = 2R$,即
$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$(规定$\sin 90^{\circ} = 1$).
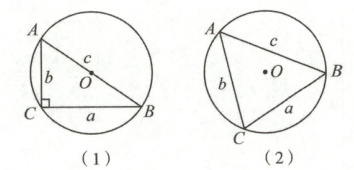
[探究活动]如图(2),在锐角$\triangle ABC$中,$a,b,c$分别是$\angle A,\angle B,\angle C$的对边,其外接圆半径
为$R$,那么$\frac{a}{\sin A} - \frac{b}{\sin B} - \frac{c}{\sin C}$(用“>”“=”或“<”连接),并说明理由.

[初步应用]事实上,以上结论适用于任意三角形.在$\triangle ABC$中,$a,b,c$分别是$\angle A,\angle B,\angle C$
的对边,$\angle B = 30^{\circ}$,$\angle C = 45^{\circ}$,$b = \sqrt{2}$,求$c$.
[综合应用]如图(3),在某次数学实践活动中,小莹同学测量一栋楼$AB$的高度,在$A$处用
测角仪测得地面点$C$处的俯角为$45^{\circ}$,点$D$处的俯角为$15^{\circ}$,$B,C,D$在一条直线上,且$C,D$
两点的距离为100米.求楼$AB$的高度.(参考数据:$\sqrt{3} \approx 1.7$,$\sin 15^{\circ} = \frac{\sqrt{6} - \sqrt{2}}{4}$)
[阅读理解]如图(1),在$ Rt\triangle ABC$中,$a,b,c$分别是$\angle A,\angle B,\angle C$的对边,$\angle C = 90^{\circ}$,其外接
圆半径为$R$.根据锐角三角函数的定义有$\sin A = \frac{a}{c}$,$\sin B = \frac{b}{c}$,可得$\frac{a}{\sin A} = \frac{b}{\sin B} = c = 2R$,即
$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$(规定$\sin 90^{\circ} = 1$).

[探究活动]如图(2),在锐角$\triangle ABC$中,$a,b,c$分别是$\angle A,\angle B,\angle C$的对边,其外接圆半径
为$R$,那么$\frac{a}{\sin A} - \frac{b}{\sin B} - \frac{c}{\sin C}$(用“>”“=”或“<”连接),并说明理由.

[初步应用]事实上,以上结论适用于任意三角形.在$\triangle ABC$中,$a,b,c$分别是$\angle A,\angle B,\angle C$
的对边,$\angle B = 30^{\circ}$,$\angle C = 45^{\circ}$,$b = \sqrt{2}$,求$c$.
[综合应用]如图(3),在某次数学实践活动中,小莹同学测量一栋楼$AB$的高度,在$A$处用
测角仪测得地面点$C$处的俯角为$45^{\circ}$,点$D$处的俯角为$15^{\circ}$,$B,C,D$在一条直线上,且$C,D$
两点的距离为100米.求楼$AB$的高度.(参考数据:$\sqrt{3} \approx 1.7$,$\sin 15^{\circ} = \frac{\sqrt{6} - \sqrt{2}}{4}$)
答案:
23.[探究活动]= =
证明:连接CO,并延长交⊙O于点D,连接BD,所以∠A=∠D,∠BDC=90°,
所以sinA=sinD.
在Rt△BCD中$,sinD=\frac{BC}{CD}=\frac{a}{2R},$
所以$\frac{a}{sinA}=\frac{a}{sinD}=\frac{a}{2R}=2R.$
同理可证$\frac{b}{sinB}=2R,\frac{c}{sinC}=2R.$
所以$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}.$
[初步应用]
因为$∠B=30°,∠C=45°,b=\sqrt{2},$
$\frac{b}{sinB}=\frac{c}{sinC},$
即$\frac{\sqrt{2}}{sin30°}=\frac{c}{sin45°}.$
所以$c=\frac{\sqrt{2}sin45°}{sin30°}=\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{\frac{1}{2}}=2.$
[综合应用]
由题意可得∠ADC=15°,∠CAD=30°,CD=100,∠ACB=45°.
在△ACD中,$\frac{CD}{sin∠CAD}=\frac{AC}{sinD},$
即$\frac{100}{sin30°}=\frac{AC}{sin15°},$
所以$AC=\frac{100sin15°}{sin30°}=\frac{100×\frac{\sqrt{6}-\sqrt{2}}{4}}{\frac{1}{2}}=100\sqrt{6}-100\sqrt{2}.$
在Rt△ABC中,
$AB=ACsin∠ACB=(100\sqrt{6}-100\sqrt{2})×\frac{\sqrt{2}}{2}=100\sqrt{3}-100=170 - 100=70,$
AB的高度大约为70米.
证明:连接CO,并延长交⊙O于点D,连接BD,所以∠A=∠D,∠BDC=90°,
所以sinA=sinD.
在Rt△BCD中$,sinD=\frac{BC}{CD}=\frac{a}{2R},$
所以$\frac{a}{sinA}=\frac{a}{sinD}=\frac{a}{2R}=2R.$
同理可证$\frac{b}{sinB}=2R,\frac{c}{sinC}=2R.$
所以$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}.$
[初步应用]
因为$∠B=30°,∠C=45°,b=\sqrt{2},$
$\frac{b}{sinB}=\frac{c}{sinC},$
即$\frac{\sqrt{2}}{sin30°}=\frac{c}{sin45°}.$
所以$c=\frac{\sqrt{2}sin45°}{sin30°}=\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{\frac{1}{2}}=2.$
[综合应用]
由题意可得∠ADC=15°,∠CAD=30°,CD=100,∠ACB=45°.
在△ACD中,$\frac{CD}{sin∠CAD}=\frac{AC}{sinD},$
即$\frac{100}{sin30°}=\frac{AC}{sin15°},$
所以$AC=\frac{100sin15°}{sin30°}=\frac{100×\frac{\sqrt{6}-\sqrt{2}}{4}}{\frac{1}{2}}=100\sqrt{6}-100\sqrt{2}.$
在Rt△ABC中,
$AB=ACsin∠ACB=(100\sqrt{6}-100\sqrt{2})×\frac{\sqrt{2}}{2}=100\sqrt{3}-100=170 - 100=70,$
AB的高度大约为70米.
查看更多完整答案,请扫码查看


