《2025年单元测试卷山东文艺出版社六年级数学上册人教版》

1. 如果只表示各种数量的多少,可以选用(条形)统计图；如果要表示出数量增减变化的情况,可以选用(折线)统计图；如果要清楚地了解各部分数量与总数之间的关系,可以选用(扇形)统计图。

答案： 条形 折线 扇形

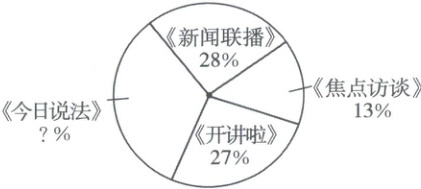
2. 如图是某学校教师喜欢看的电视节目统计图。喜欢看《今日说法》的教师占全体教师人数的(32)%；喜欢看(《新闻联播》)节目和(《开讲啦》)节目的人数差不多；喜欢看(《焦点访谈》)节目的人数最少；如果该学校有150名教师,那么喜欢看《新闻联播》的教师有(42)人。

答案： 32 《新闻联播》《开讲啦》《焦点访谈》 42

3. (1)观察一组等式：$2×4= 3^{2}-1$,$3×5= 4^{2}-1$,$4×6= 5^{2}-1$,$10×12= 11^{2}-1$
找规律填空：$2023×2025=$($2024^{2}-1$)；
(2)请把你猜想的规律用含有字母$n$的式子表示：$n×(n+2)=$($(n+1)^{2}-1$)。

答案：
(1)$2024^{2}-1$；
(2)$(n+1)^{2}-1$

4. 从下图中点的排列规律可以看出,第5幅图共有(16)个点,第$n$幅图共有($3n+1$)个点。

答案： 16 $3n+1$

5. $1+3+5+7+9+11+13+15+13+11+9+7+5+3+1=$(113)。

答案： 113

6. $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}=$($\frac {127}{128}$)。

答案： $\frac {127}{128}$

7. A、B、C、D、E五个人参加羽毛球单打比赛,每两个人都要打一局,到现在为止,A打了4局,B打了3局,C打了2局,D打了1局,E打了(2)局。

答案： 2

8. (推理意识)观察下图并填空。

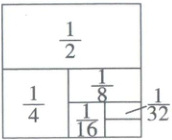
$1-\frac{1}{2}= \frac{1}{2}$ $1-\frac{1}{2}-\frac{1}{4}= \frac{1}{4}$
$1-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}= \frac{1}{8}$ $1-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}=$($\frac {1}{16}$)
$1-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-…-\frac{1}{256}=$($\frac {1}{256}$)

答案： $\frac {1}{16}$ $\frac {1}{256}$