第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
三、我能行。(12分)
李老师对六(3)班学生期中考试数学成绩进行了统计,统计结果如下表所示:
六(3)班学生期中考试数学成绩统计表

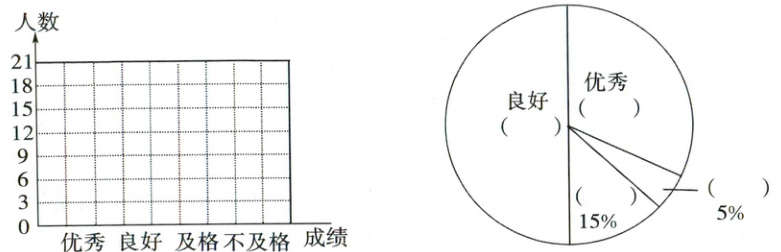
请你根据统计表,把下面的条形统计图和扇形统计图补充完整。
1. 总人数:$12 + 20 + 6 + 2$
$=32 + 6 + 2 + 12-12$(加法结合律)
$= 40$(人)
优秀占比:$\frac{12}{40} × 100\% = 30\%$,
及格占比:$\frac{6}{40} × 100\% = 15\%$,
不及格占比:$\frac{2}{40} × 100\% = 5\%$,
良好占比:$\frac{20}{40} × 100\% = 50\%$。
条形统计图:优秀对应 12 人,良好对应 20 人,及格对应 6 人,不及格对应 2 人,在条形统计图相应位置画出对应高度的直条。
扇形统计图:优秀对应$30\%$,良好对应$50\%$,及格对应$15\%$,不及格对应$5\%$,在扇形统计图相应区域标出对应比例。
李老师对六(3)班学生期中考试数学成绩进行了统计,统计结果如下表所示:
六(3)班学生期中考试数学成绩统计表

请你根据统计表,把下面的条形统计图和扇形统计图补充完整。

1. 总人数:$12 + 20 + 6 + 2$
$=32 + 6 + 2 + 12-12$(加法结合律)
$= 40$(人)
优秀占比:$\frac{12}{40} × 100\% = 30\%$,
及格占比:$\frac{6}{40} × 100\% = 15\%$,
不及格占比:$\frac{2}{40} × 100\% = 5\%$,
良好占比:$\frac{20}{40} × 100\% = 50\%$。
条形统计图:优秀对应 12 人,良好对应 20 人,及格对应 6 人,不及格对应 2 人,在条形统计图相应位置画出对应高度的直条。
扇形统计图:优秀对应$30\%$,良好对应$50\%$,及格对应$15\%$,不及格对应$5\%$,在扇形统计图相应区域标出对应比例。
答案:
1. 总人数:$12 + 20 + 6 + 2$
$=32 + 6 + 2 + 12-12$(加法结合律)
$= 40$(人)
优秀占比:$\frac{12}{40} × 100\% = 30\%$,
及格占比:$\frac{6}{40} × 100\% = 15\%$,
不及格占比:$\frac{2}{40} × 100\% = 5\%$,
良好占比:$\frac{20}{40} × 100\% = 50\%$。
条形统计图:优秀对应 12 人,良好对应 20 人,及格对应 6 人,不及格对应 2 人,在条形统计图相应位置画出对应高度的直条。
扇形统计图:优秀对应$30\%$,良好对应$50\%$,及格对应$15\%$,不及格对应$5\%$,在扇形统计图相应区域标出对应比例。
$=32 + 6 + 2 + 12-12$(加法结合律)
$= 40$(人)
优秀占比:$\frac{12}{40} × 100\% = 30\%$,
及格占比:$\frac{6}{40} × 100\% = 15\%$,
不及格占比:$\frac{2}{40} × 100\% = 5\%$,
良好占比:$\frac{20}{40} × 100\% = 50\%$。
条形统计图:优秀对应 12 人,良好对应 20 人,及格对应 6 人,不及格对应 2 人,在条形统计图相应位置画出对应高度的直条。
扇形统计图:优秀对应$30\%$,良好对应$50\%$,及格对应$15\%$,不及格对应$5\%$,在扇形统计图相应区域标出对应比例。
1. 六(2)班共有50名学生,他们分别参加了足球、乒乓球、英语、篮球及摄影兴趣小组且每一个学生只参加其中一个兴趣小组。(12分)

(1) 参加足球、乒乓球、篮球小组的学生各有多少人?
(2) 参加足球小组的学生比参加乒乓球小组的学生多百分之几?
(3) 请再提出一个数学问题并解答。

(1) 参加足球、乒乓球、篮球小组的学生各有多少人?
(2) 参加足球小组的学生比参加乒乓球小组的学生多百分之几?
(3) 请再提出一个数学问题并解答。
答案:
(1)足球:$50× 30\% =15$(人) 乒乓球:$50× 20\% =10$(人) 篮球:$50× 24\% =12$(人)
(2)$(15-10)÷ 10=0.5=50\% $
(3)略。
(1)足球:$50× 30\% =15$(人) 乒乓球:$50× 20\% =10$(人) 篮球:$50× 24\% =12$(人)
(2)$(15-10)÷ 10=0.5=50\% $
(3)略。
2. 变速跑有助于培养精神韧性和耐力,第一阶段慢跑热身,第二阶段提速长跑,第三阶段快速冲刺。如图是淘淘同学在“变速跑”晨练中的行程情况和时间分配情况。(12分)
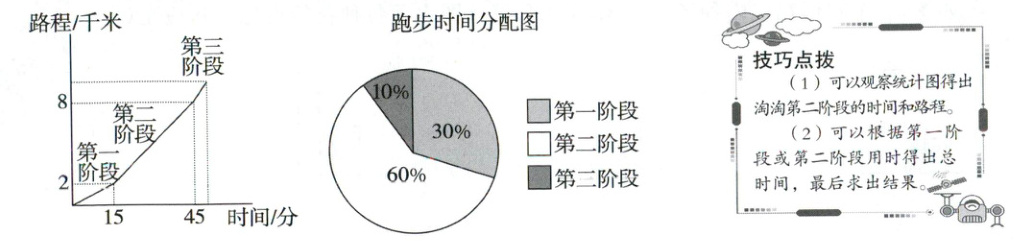
(1) 根据图中的折线统计图算一算,淘淘在第二阶段的速度是多少?
(2) 结合两幅图分析一下,淘淘第三阶段用时多少?

(1) 根据图中的折线统计图算一算,淘淘在第二阶段的速度是多少?
(2) 结合两幅图分析一下,淘淘第三阶段用时多少?
答案:
(1)$(8-2)÷ (45-15)=0.2$(千米/分) 淘淘在第二阶段的速度是0.2千米/分。
(2)$15÷ 30\% × 10\% =5$(分钟) 淘淘第三阶段用时5分钟。
(1)$(8-2)÷ (45-15)=0.2$(千米/分) 淘淘在第二阶段的速度是0.2千米/分。
(2)$15÷ 30\% × 10\% =5$(分钟) 淘淘第三阶段用时5分钟。
查看更多完整答案,请扫码查看


