第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
3. 把一个圆等分后剪拼成一个近似的梯形,这个梯形的周长大约是21.42cm,则圆的面积是多少?(π取3.14)(6分)
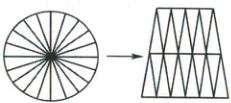

答案:
设圆的半径为r cm。2×3.14×(10/20)r+4r=21.42 r=3 3.14×3²=28.26(cm²)
4. 如图,$AB = BC = CD = 4$厘米,$∠ABC和∠BCD$都是直角。一枚半径为1厘米的游戏币从点A出发,沿$A—BC—D$的路径无滑动地滚动到点D。(8分)
(1)计算游戏币从A滚动到D的过程中圆心走过的路径长度。
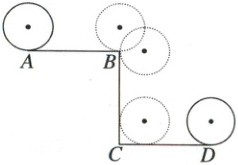
(2)游戏币从A滚动到C的过程中扫过的面积是多少?
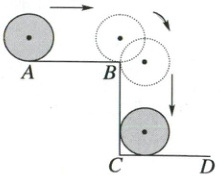
(1)计算游戏币从A滚动到D的过程中圆心走过的路径长度。

(2)游戏币从A滚动到C的过程中扫过的面积是多少?

答案:
(1)4+1/4×2×3.14×1+(4-1)×2=11.57(厘米)
(2)3.14×1²+4×2+1/4×3.14×2²+(4-1)×2=20.28(平方厘米)
(1)4+1/4×2×3.14×1+(4-1)×2=11.57(厘米)
(2)3.14×1²+4×2+1/4×3.14×2²+(4-1)×2=20.28(平方厘米)
七、智慧乐园。(6分)
如图,大圆的半径为$R$,小圆的半径为$r$,阴影部分的面积是20平方厘米,圆环的面积是多少?
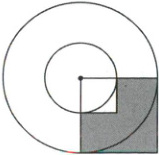
如图,大圆的半径为$R$,小圆的半径为$r$,阴影部分的面积是20平方厘米,圆环的面积是多少?

答案:
阴影部分的面积为R²-r²=20(平方厘米) 圆环的面积为π(R²-r²)=62.8(平方厘米)
查看更多完整答案,请扫码查看


