20. 【情境再现】
甲、乙两个含$45^{\circ}$角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足$O$处.将甲绕点$O$顺时针旋转一定角度到图②位置.小莹用作图软件按图②作出示意图,并连接$AG$,$BH$,$AO$,如图③所示,$AB交HO于点E$,$AC交OG于点F$,$\triangle OBE\cong \triangle OAF$.
 求证$AG = BH$.
求证$AG = BH$.
【迁移应用】
延长$GA分别交HO$,$HB于点P$,$D$,如图④,猜想并证明$DG与BH$的位置关系.
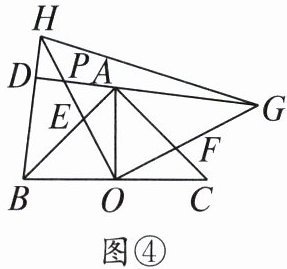
甲、乙两个含$45^{\circ}$角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足$O$处.将甲绕点$O$顺时针旋转一定角度到图②位置.小莹用作图软件按图②作出示意图,并连接$AG$,$BH$,$AO$,如图③所示,$AB交HO于点E$,$AC交OG于点F$,$\triangle OBE\cong \triangle OAF$.
 求证$AG = BH$.
求证$AG = BH$.【迁移应用】
延长$GA分别交HO$,$HB于点P$,$D$,如图④,猜想并证明$DG与BH$的位置关系.

答案:
【情境再现】证明 由阅读材料知△OBE≌△OAF,
∴BE=AF,OE=OF,∠BEO=∠AFO,
∴∠BEH=∠AFG.
∵OH=OG,
∴OH - OE=OG - OF,即EH=GF.
∵在△BHE和△AGF中,$\left\{\begin{array}{l} BE=AF,\\ ∠BEH=∠AFG,\\ EH=FG,\end{array}\right. $
∴△BHE≌△AGF(SAS),
∴BH=AG.【迁移应用】解 猜想:DG⊥BH.证明:由【情境再现】知,△BHE≌△AGF,
∴∠BHE=∠AGF.
∵∠HOG=90°,
∴∠AGF+∠GPO=90°,
∴∠BHE+∠GPO=90°.
∵∠GPO=∠HPD,
∴∠BHE+∠HPD=90°,
∴∠HDP=90°,
∴DG⊥BH.
∴BE=AF,OE=OF,∠BEO=∠AFO,
∴∠BEH=∠AFG.
∵OH=OG,
∴OH - OE=OG - OF,即EH=GF.
∵在△BHE和△AGF中,$\left\{\begin{array}{l} BE=AF,\\ ∠BEH=∠AFG,\\ EH=FG,\end{array}\right. $
∴△BHE≌△AGF(SAS),
∴BH=AG.【迁移应用】解 猜想:DG⊥BH.证明:由【情境再现】知,△BHE≌△AGF,
∴∠BHE=∠AGF.
∵∠HOG=90°,
∴∠AGF+∠GPO=90°,
∴∠BHE+∠GPO=90°.
∵∠GPO=∠HPD,
∴∠BHE+∠HPD=90°,
∴∠HDP=90°,
∴DG⊥BH.
21. 如图,在$\triangle ABC$中,点$D在边BC$的延长线上,$\angle ACB = 108^{\circ}$,$BE平分\angle ABC交AD于点E$,过点$E作EH\perp BD$,垂足为$H$,$\angle CEH = 54^{\circ}$.
(1)求$\angle ACE$的度数;
(2)请判断$AE是否平分\angle CAF$,并说明理由;
(3)若$AC + CD = 10$,$AB = 6$,且$S_{\triangle ACD}= 15$,求$\triangle ABE$的面积.
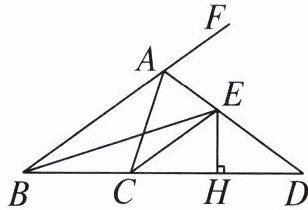
(1)求$\angle ACE$的度数;
(2)请判断$AE是否平分\angle CAF$,并说明理由;
(3)若$AC + CD = 10$,$AB = 6$,且$S_{\triangle ACD}= 15$,求$\triangle ABE$的面积.

答案:
解
(1)
∵∠ACB=108°,
∴∠ACD=180° - 108°=72°.
∵EH⊥BD,
∴∠CHE=90°.
∵∠CEH=54°,
∴∠ECH=90° - 54°=36°,
∴∠ACE=72° - 36°=36°.
(2)AE平分∠CAF,理由:如图,过点E分别作EM⊥BF于点M,EN⊥AC于点N,
∵BE平分∠ABC,
∴EM=EH.
∵由
(1)知∠ACE=∠ECH=36°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF.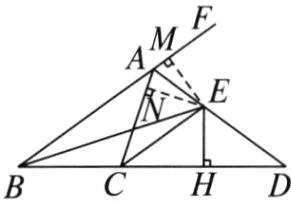
(3)
∵AC+CD=10,S△ACD=15,且由
(2)知EM=EN=EH,
∴S△ACD=S△ACE+S△CED=$\frac {1}{2}$AC·EN+$\frac {1}{2}$CD·EH=$\frac {1}{2}$(AC+CD)·EM=15,即$\frac {1}{2}$×10·EM=15,解得EM=3.
∵AB=6,
∴S△ABE=$\frac {1}{2}$AB·EM=$\frac {1}{2}$×6×3=9.
解
(1)
∵∠ACB=108°,
∴∠ACD=180° - 108°=72°.
∵EH⊥BD,
∴∠CHE=90°.
∵∠CEH=54°,
∴∠ECH=90° - 54°=36°,
∴∠ACE=72° - 36°=36°.
(2)AE平分∠CAF,理由:如图,过点E分别作EM⊥BF于点M,EN⊥AC于点N,
∵BE平分∠ABC,
∴EM=EH.
∵由
(1)知∠ACE=∠ECH=36°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF.

(3)
∵AC+CD=10,S△ACD=15,且由
(2)知EM=EN=EH,
∴S△ACD=S△ACE+S△CED=$\frac {1}{2}$AC·EN+$\frac {1}{2}$CD·EH=$\frac {1}{2}$(AC+CD)·EM=15,即$\frac {1}{2}$×10·EM=15,解得EM=3.
∵AB=6,
∴S△ABE=$\frac {1}{2}$AB·EM=$\frac {1}{2}$×6×3=9.
查看更多完整答案,请扫码查看


