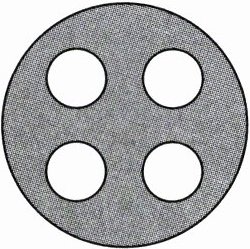
20. 如图,小刚家门口的商店在装修,他发现工人师傅在一块半径为$R的圆形板材上剪出四个半径为r$的小圆,小刚测得$R = 6.8dm$,$r = 1.6dm$,他想知道剩余部分(阴影部分)的面积,你能利用所学过的因式分解的知识帮助小刚吗?请写出求解过程.(结果保留$\pi$)

答案:
根据题意,得剩余部分的面积为πR²-4πr²=π(R²-4r²)=π(R+2r)(R-2r).当R=6.8,r=1.6时,原式=π×(6.8+3.2)×(6.8-3.2)=36π.即剩余部分的面积为36π dm².
21. 阅读材料:利用公式法,可以将一些形如$ax^{2} + bx + c(a ≠ 0)的多项式变形为a(x + m)^{2} + n$的形式,我们把这样的变形方法叫作多项式$ax^{2} + bx + c(a ≠ 0)$的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解.例如$x^{2} + 4x - 5 = x^{2} + 4x + (\frac{4}{2})^{2} - (\frac{4}{2})^{2} - 5 = (x + 2)^{2} - 9 = (x + 2 + 3)(x + 2 - 3) = (x + 5)(x - 1)$.根据以上材料,解答下列问题:
(1)分解因式(利用配方法):$x^{2} - 4x - 12$;
(2)求多项式$x^{2} + 4x - 3$的最小值;
(3)已知$a$,$b$,$c是\triangle ABC$的三边长,且满足$a^{2} + b^{2} + c^{2} + 50 = 6a + 8b + 10c$,求$\triangle ABC$的周长.
(1)分解因式(利用配方法):$x^{2} - 4x - 12$;
(2)求多项式$x^{2} + 4x - 3$的最小值;
(3)已知$a$,$b$,$c是\triangle ABC$的三边长,且满足$a^{2} + b^{2} + c^{2} + 50 = 6a + 8b + 10c$,求$\triangle ABC$的周长.
答案:
(1)原式=x²-4x+4-4-12=(x-2)²-16=(x-2+4)(x-2-4)=(x+2)(x-6);
(2)原式=x²+4x+4-4-3=(x+2)²-7.
∵(x+2)²≥0,
∴(x+2)²-7≥-7,
∴多项式x²+4x-3的最小值为-7;
(3)由题意可得a²+b²+c²+50-6a-8b-10c=0,
∴a²-6a+9+b²-8b+16+c²-10c+25-9-16-25+50=0,
∴(a-3)²+(b-4)²+(c-5)²=0,
∴a-3=0,b-4=0,c-5=0,
∴a=3,b=4,c=5,
∴a+b+c=3+4+5=12,即△ABC的周长为12.
(1)原式=x²-4x+4-4-12=(x-2)²-16=(x-2+4)(x-2-4)=(x+2)(x-6);
(2)原式=x²+4x+4-4-3=(x+2)²-7.
∵(x+2)²≥0,
∴(x+2)²-7≥-7,
∴多项式x²+4x-3的最小值为-7;
(3)由题意可得a²+b²+c²+50-6a-8b-10c=0,
∴a²-6a+9+b²-8b+16+c²-10c+25-9-16-25+50=0,
∴(a-3)²+(b-4)²+(c-5)²=0,
∴a-3=0,b-4=0,c-5=0,
∴a=3,b=4,c=5,
∴a+b+c=3+4+5=12,即△ABC的周长为12.
查看更多完整答案,请扫码查看


