9. 如图,将三角形纸片$ABC沿DE$折叠,点$A落在点F$处,若$\angle 1+\angle 2 = 108^{\circ}$,则$\angle A$的度数为( )

A.$72^{\circ}$
B.$54^{\circ}$
C.$36^{\circ}$
D.$108^{\circ}$

A.$72^{\circ}$
B.$54^{\circ}$
C.$36^{\circ}$
D.$108^{\circ}$
答案:
B
10. 如图,在$\triangle ABC$中,$O$是三个内角的平分线的交点,过点$O作\angle ODC= \angle AOC$,交边$BC于点D$.若$\angle ABC = n^{\circ}$,则$\angle BOD$的度数为( )

A.$90^{\circ}+\frac{1}{2}n^{\circ}$
B.$45^{\circ}+\frac{1}{2}n^{\circ}$
C.$90^{\circ}-\frac{1}{2}n^{\circ}$
D.$90^{\circ}$

A.$90^{\circ}+\frac{1}{2}n^{\circ}$
B.$45^{\circ}+\frac{1}{2}n^{\circ}$
C.$90^{\circ}-\frac{1}{2}n^{\circ}$
D.$90^{\circ}$
答案:
D
11. 已知$a$,$b$,$c$是一个三角形的三条边长.化简$\vert a + b - c\vert-\vert a - b + c\vert+\vert a - b - c\vert=$______.
答案:
-a+3b-c
12. 如图,经测量,$B处在A处的南偏西60^{\circ}$方向,$C处在A处的南偏东20^{\circ}$方向,$BE$为正北方向,$AD$为正南方向,$\angle CBE = 100^{\circ}$,则$\angle ACB$的度数是______.
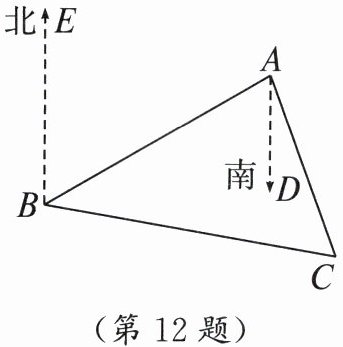

答案:
60°
13. 如图,已知$AD是\triangle ABC$的中线,$BE是\triangle ABD$的中线,若$\triangle ABC的面积为16$,则$\triangle ABE$的面积为______.


答案:
4
14. 如图,已知$EF与BD的延长线相交于点P$,$AB// CD$,$\angle P = 15^{\circ}$,$\angle CFP = 100^{\circ}$,则$\angle ABP$的大小为______.
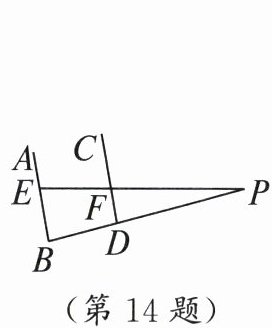

答案:
85°
15. 如图,小明在计算机上用“几何画板”画了一个$\mathrm{Rt}\triangle ABC$,$\angle C = 90^{\circ}$,并画出了两锐角的平分线$AD$,$BE及其交点F$.小明发现,无论怎样变动$\mathrm{Rt}\triangle ABC$的形状和大小,$\angle AFB$的度数是定值.这个定值为______.


答案:
135°
16. 如果三角形的两个内角$\alpha与\beta满足\alpha+3\beta = 90^{\circ}$,那么我们称这样的三角形为“准直角三角形”.如图,$B$,$C为直线l$上两点,点$A在直线l$外,且$\angle ABC = 42^{\circ}$,若$P是l$上一点,且$\triangle ABP$是“准直角三角形”,则$\angle APB$的所有可能的度数为______.


答案:
16°或18°或24°或122°
查看更多完整答案,请扫码查看


