11. 计算$(a^{3})^{2} ÷ (a^{2})^{3}$的结果等于______。
答案:
1
12. 若多项式$x^{2}-2(k - 1)x + 9$是一个完全平方式,则常数$k$的值为______。
答案:
4或-2
13. 若一个多项式$M与单项式2x^{2}的积是10x^{4}-8x^{5}$,则这个多项式$M$是______。
答案:
$5x^{2}-4x^{3}$
14. 若$2^{2n + 3}+4^{n + 1}= 192$,则$n$的值为______。
答案:
2
15. 若$(x^{2}+ax + 3)(x + 4)的展开式中不含x$的一次项,则常数$a$的值为______。
答案:
$-\frac{3}{4}$
16. 如图,从边长为$(m + 3)的正方形纸片上剪出一个边长为m$的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为$3$,则另一边长为______。
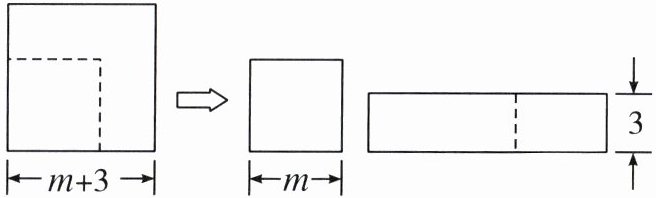

答案:
$2m+3$
17. 计算:
(1)$2x^{2}y \cdot (-3xy^{2})^{3}$;
(2)$(12a^{3}-7a^{2}+5a) ÷ 3a$;
(3)$(x + 1)(x - 3)-(x + 1)^{2}$;
(4)$(-x + 4y)(-x - 4y)$。
(1)$2x^{2}y \cdot (-3xy^{2})^{3}$;
(2)$(12a^{3}-7a^{2}+5a) ÷ 3a$;
(3)$(x + 1)(x - 3)-(x + 1)^{2}$;
(4)$(-x + 4y)(-x - 4y)$。
答案:
(1)原式$=2x^{2}y\cdot(-27x^{3}y^{6})=-54x^{5}y^{7}$.
(2)原式$=4a^{2}-\frac{7}{3}a+\frac{5}{3}$.
(3)原式$=x^{2}-3x+x-3-(x^{2}+2x+1)$
$=x^{2}-3x+x-3-x^{2}-2x-1=-4x-4$.
(4)原式$=x^{2}-16y^{2}$.
(2)原式$=4a^{2}-\frac{7}{3}a+\frac{5}{3}$.
(3)原式$=x^{2}-3x+x-3-(x^{2}+2x+1)$
$=x^{2}-3x+x-3-x^{2}-2x-1=-4x-4$.
(4)原式$=x^{2}-16y^{2}$.
查看更多完整答案,请扫码查看


