《2025年同步测控优化设计八年级数学上册人教版福建专版》

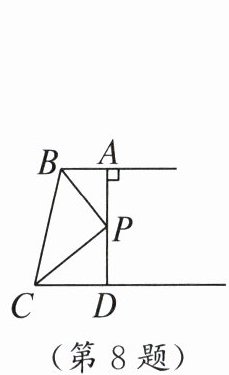
8. 如图,$AB// CD$,$BP和CP分别平分\angle ABC和\angle DCB$,$AD过点P$,且与$AB$垂直.若$AD = 8$,则点$P到BC$的距离是( )

A.$8$
B.$6$
C.$4$
D.$2$

答案： C

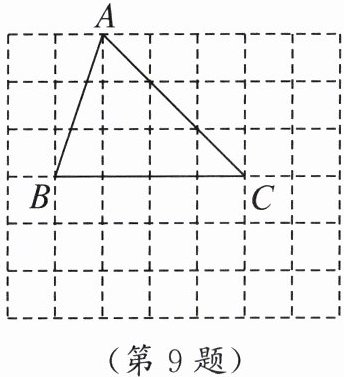
9. 如图,在一个正方形网格中,每个网格正方形的边长相等,我们把该网格中正方形的顶点称之为“好点”,$\triangle ABC$的三个顶点都在这个正方形网格的“好点”上,在这个正方形网格图中找一个“好点”$D$(点$D与点A$不重合),使得以$D$,$B$,$C为顶点的三角形与\triangle ABC$全等,则这样的“好点”$D$的个数为( )

A.$1$
B.$2$
C.$3$
D.$4$

答案： C

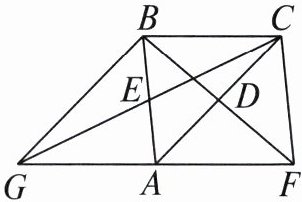
10. 如图,在$\triangle ABC$中,分别延长$AC$,$AB边上的中线BD$,$CE到点F$,$G$,使$DF = BD$,$EG = CE$,有下列说法：①$GA = AF$；②$GA// BC$；③$GB = AC$；④四边形$GBCF的面积是\triangle ABC面积的3$倍.其中正确的个数是( )


A.$1$
B.$2$
C.$3$
D.$4$

答案： D

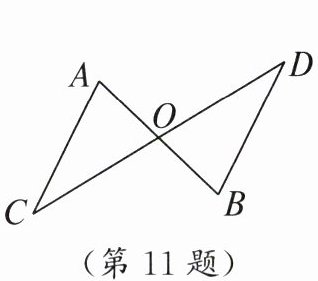
11. 如图,$AB$,$CD相交于点O$,$AO = OB$,观察图形,只需补充一个条件______,可得到$\triangle AOC\cong \triangle BOD$.

答案： OC=OD(答案不唯一)

12. 如图,$\triangle ABC\cong \triangle A^{\prime}BC^{\prime}$,过点$C作CD\perp BC^{\prime}$,垂足为$D$,若$\angle ABA^{\prime}=55^{\circ}$,则$\angle BCD$的度数为______.

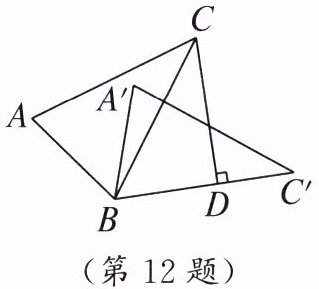
答案： 35°

13. 在平面直角坐标系的$x$轴、$y轴上分别截取OA = OB$,再分别以点$A$,$B$为圆心,以大于$\frac{1}{2}AB$长为半径画弧,两弧交于点$P$,若点$P的坐标为(a,2)$,则$a$的值是______.

答案： 2或-2

14. 如图,在由$4$个相同的小正方形组成的网格图中,$\angle 1+\angle 2$等于______.

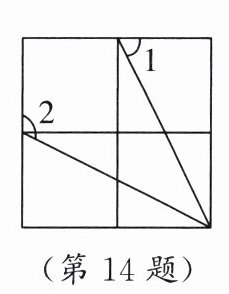
答案： 180°

15. 如图,$AB// CD$,$O为\angle BAC$,$\angle ACD$的平分线的交点,$OE\perp AC于点E$,且$OE = 1$,则$AB与CD$之间的距离等于______.

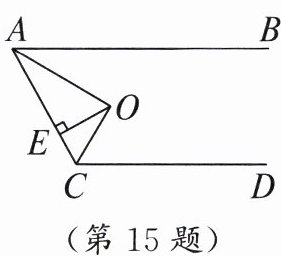
答案： 2

16. 如图,$\angle C = 90^{\circ}$,$AC = 10$,$BC = 5$,$AX\perp AC$,点$P和点Q同时从点A$出发,分别在线段$AC和射线AX$上运动,且$AB = PQ$(不考虑$PQ = 0$的情况),当点$P运动到AP = $______时,$\triangle ABC与\triangle APQ$全等.

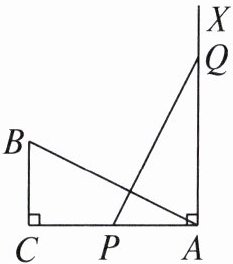
答案： 5或10