20. 如图,某小区有一块长$(2a + 4b)$m,宽$(2a - b)$m的长方形地块,角上有四个边长为$(a - b)$m的小正方形空地,开发商计划将阴影部分进行绿化。
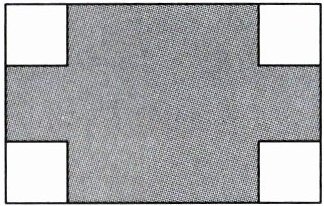
(1)用含有$a$,$b$的式子表示绿化面积(结果写成最简形式);
(2)物业找来某绿化团队完成此项绿化任务,已知该团队每小时可绿化$8b$ $m^{2}$,每小时收费$200$元,则该物业应该支付多少绿化费用?(用含$a$,$b$的代数式表示)

(1)用含有$a$,$b$的式子表示绿化面积(结果写成最简形式);
(2)物业找来某绿化团队完成此项绿化任务,已知该团队每小时可绿化$8b$ $m^{2}$,每小时收费$200$元,则该物业应该支付多少绿化费用?(用含$a$,$b$的代数式表示)
答案:
(1)根据题意,得
$(2a-b)(2a+4b)-4(a-b)^{2}$
$=4a^{2}+8ab-2ab-4b^{2}-4(a^{2}-2ab+b^{2})$
$=4a^{2}+6ab-4b^{2}-4a^{2}+8ab-4b^{2}$
$=(14ab-8b^{2})(m^{2})$.
故绿化面积是$(14ab-8b^{2})m^{2}$.
(2)根据题意,得$(14ab-8b^{2})÷(8b)×200=\left(\frac{7}{4}a-b\right)×200=(350a-200b)$(元).
答:该物业应该支付$(350a-200b)$元绿化费用.
$(2a-b)(2a+4b)-4(a-b)^{2}$
$=4a^{2}+8ab-2ab-4b^{2}-4(a^{2}-2ab+b^{2})$
$=4a^{2}+6ab-4b^{2}-4a^{2}+8ab-4b^{2}$
$=(14ab-8b^{2})(m^{2})$.
故绿化面积是$(14ab-8b^{2})m^{2}$.
(2)根据题意,得$(14ab-8b^{2})÷(8b)×200=\left(\frac{7}{4}a-b\right)×200=(350a-200b)$(元).
答:该物业应该支付$(350a-200b)$元绿化费用.
21. 完全平方公式经过适当的变形,可以解决很多数学问题。例如:
若$a + b = 3$,$ab = 1$,求$a^{2}+b^{2}$的值。
解:$\because a + b = 3$,$ab = 1$,
$\therefore (a + b)^{2}= 9$,即$a^{2}+b^{2}+2ab = 9$,
$\therefore a^{2}+b^{2}= 7$。
根据上面的解题思路与方法解决下列问题:
(1)$a + b = 5$,$ab = 1$,则$a^{2}+b^{2}$的值为______;
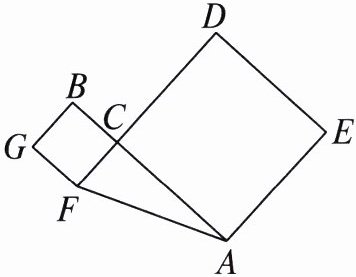
(2)如图,$C是线段AB$上的一点,分别以$AC$,$BC$为边向两边作正方形,设$AB = 6$,两正方形的面积和为$20$,求$\triangle AFC$的面积;
(3)若$(10 - x)(x - 6)= 1$,求$(10 - x)^{2}+(x - 6)^{2}$的值。
若$a + b = 3$,$ab = 1$,求$a^{2}+b^{2}$的值。
解:$\because a + b = 3$,$ab = 1$,
$\therefore (a + b)^{2}= 9$,即$a^{2}+b^{2}+2ab = 9$,
$\therefore a^{2}+b^{2}= 7$。
根据上面的解题思路与方法解决下列问题:
(1)$a + b = 5$,$ab = 1$,则$a^{2}+b^{2}$的值为______;
(2)如图,$C是线段AB$上的一点,分别以$AC$,$BC$为边向两边作正方形,设$AB = 6$,两正方形的面积和为$20$,求$\triangle AFC$的面积;
(3)若$(10 - x)(x - 6)= 1$,求$(10 - x)^{2}+(x - 6)^{2}$的值。

答案:
(1)23
(2)设大正方形的边长为$a$,小正方形的边长为$b$,根据题意可知$a+b=6$,$a^{2}+b^{2}=20$,$\therefore(a+b)^{2}=36$,
即$a^{2}+b^{2}+2ab=36$,$\therefore2ab=36-20=16$,
$\therefore ab=8$,$\therefore S_{\triangle AFC}=\frac{1}{2}ab=\frac{1}{2}×8=4$.
(3)$\because(10-x)(x-6)=1$,
$\therefore(10-x)^{2}+(x-6)^{2}=[(10-x)+(x-6)]^{2}-2(10-x)(x-6)=4^{2}-2×1=14$.
(2)设大正方形的边长为$a$,小正方形的边长为$b$,根据题意可知$a+b=6$,$a^{2}+b^{2}=20$,$\therefore(a+b)^{2}=36$,
即$a^{2}+b^{2}+2ab=36$,$\therefore2ab=36-20=16$,
$\therefore ab=8$,$\therefore S_{\triangle AFC}=\frac{1}{2}ab=\frac{1}{2}×8=4$.
(3)$\because(10-x)(x-6)=1$,
$\therefore(10-x)^{2}+(x-6)^{2}=[(10-x)+(x-6)]^{2}-2(10-x)(x-6)=4^{2}-2×1=14$.
查看更多完整答案,请扫码查看


