《2025年新课程课堂同步练习册九年级数学上册人教版》

1. 抛物线$y= -3(x-1)^{2}-2$的对称轴是直线$x=1$.

答案： 直线$x=1$

2. 抛物线$y= -5x^{2}+19x+6与y$轴的交点坐标为$(0,6)$.

答案： 解：将$x=0$代入$y= -5x^{2}+19x+6$，得：
$y = -5×(0)^{2} + 19×(0) + 6 = 6$，
所以，抛物线与y轴的交点坐标为$(0,6)$。
故答案为：$(0,6)$。

3. 已知点$(-1,2)在二次函数y= kx^{2}$的图象上,则$k$的值是2.

答案： 解：因为点$(-1,2)$在二次函数$y=kx^{2}$的图象上，所以将$x=-1$，$y=2$代入函数解析式可得：$2=k×(-1)^{2}$，即$2=k×1$，解得$k=2$。
2

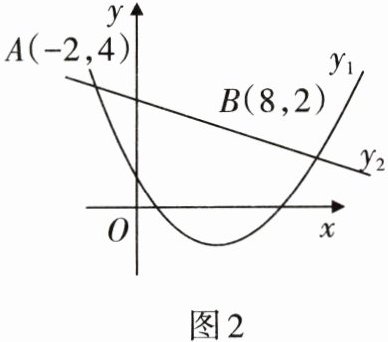
4. 如图2,已知二次函数$y_{1}= ax^{2}+bx+c(a＞0)与一次函数y_{2}= kx+m(k≠0)的图象相交于点A(-2,4)$,$B(8,2)$,则使$y_{1}＞y_{2}成立的x$的取值范围是$x\lt -2$或$x\gt 8$.

答案： $x\lt -2$或$x\gt 8$

1. 已知一次函数$y= -2x+c与二次函数y= ax^{2}+bx-4(a≠0)的图象都经过点A(1,-1)$,且二次函数的对称轴是直线$x= -1$.
(1)请求出一次函数和二次函数的解析式；
(2)指出二次函数值大于一次函数值时的自变量$x$的取值范围(直接写出答案).

答案：
(1)解：将点A(1,-1)代入一次函数$y=-2x+c$，得$-1=-2×1+c$，解得$c=1$，所以一次函数解析式为$y=-2x+1$。
将点A(1,-1)代入二次函数$y=ax^{2}+bx-4$，得$a+b-4=-1$，即$a+b=3$。
因为二次函数对称轴是直线$x=-1$，所以$-\frac{b}{2a}=-1$，即$b=2a$。
联立$\begin{cases}a+b=3\\b=2a\end{cases}$，解得$\begin{cases}a=1\\b=2\end{cases}$，所以二次函数解析式为$y=x^{2}+2x-4$。
(2)$x＜-3$或$x＞1$