《2025年新课程课堂同步练习册九年级数学上册人教版》

2. 从1名男生和2名女生中随机抽取参加“我爱我家乡”演讲赛的学生,求下列事件的概率：
(1)抽取1名,恰好是男生；
(2)抽取2名,恰好是1名女生和1名男生.

答案：
(1) 解：总共有3名学生（1名男生和2名女生），所以抽取1名恰好是男生的概率为：
$P(恰好是男生) = \frac{男生人数}{总人数} = \frac{1}{3}$
(2) 解：从3名学生中随机抽取2名学生的组合数为$C_{3}^{2} = \frac{3!}{2!(3-2)!} = 3$，
从1名男生中选1名，和从2名女生中选1名的组合数为$C_{1}^{1} × C_{2}^{1} = 1 × 2 = 2$，
所以，抽取2名学生，恰好是1名女生和1名男生的概率为：
$P(恰好是1名女生和1名男生) = \frac{C_{1}^{1} × C_{2}^{1}}{C_{3}^{2}} = \frac{2}{3}$。

3. 在一个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外其他都相同),其中有白球2个、黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球不放回,再摸出一个.请用画树状图的方法求甲摸到两个球共得2分的概率.

答案：
解：
(1)设袋中有红球x个，则有
$ \frac 2 {2+1+x}=0.5$
解得，x=1
∴袋中有红球1个
(2)画树状图如下：

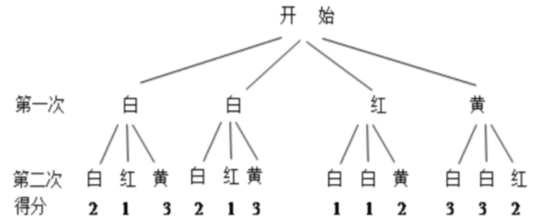
共有12种等可能的结果，其中共得2分的结果有4种．
∴P(甲摸到两个球共得2分$)=\frac 4 {12}=\frac 1 3$