《2025年新课程课堂同步练习册九年级数学上册人教版》

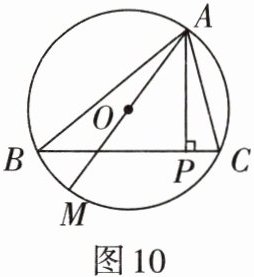
2. 如图10,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径. 求证:∠BAM= ∠CAP.

答案： 证明：
连接$BM$。
$\because AM$为$\odot O$的直径，
$\therefore \angle ABM=90^\circ$，
$\therefore \angle BAM+\angle AMB=90^\circ$，
$\because AP \perp BC$，
$\therefore \angle APC=90^\circ$，
$\therefore \angle CAP+\angle C=90^\circ$，
$\because \angle AMB=\angle C$（同弧所对的圆周角相等），
$\therefore \angle BAM=\angle CAP$。

3. 已知等腰三角形ABC内接于半径为6 cm的⊙O,AB= AC,点O到BC的距离OD的长等于2 cm.求AB的长.

答案： 解：连接OB，OA，延长AO交BC于点D，由AB=AC得AD⊥BC，OD=2cm，OB=6cm。
情况一：圆心O在△ABC内部。
OD=2cm，OB=6cm，在Rt△OBD中，BD²=OB²-OD²=6²-2²=32，BD=4√2cm。
AD=AO+OD=6+2=8cm，在Rt△ABD中，AB²=AD²+BD²=8²+(4√2)²=64+32=96，AB=4√6cm。
情况二：圆心O在△ABC外部。
OD=2cm，OB=6cm，在Rt△OBD中，BD²=OB²-OD²=6²-2²=32，BD=4√2cm。
AD=AO-OD=6-2=4cm，在Rt△ABD中，AB²=AD²+BD²=4²+(4√2)²=16+32=48，AB=4√3cm。
综上，AB的长为4√6cm或4√3cm。