《2025年新课程课堂同步练习册九年级数学上册人教版》

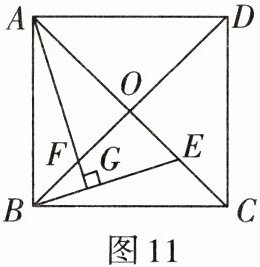
3. 如图11,正方形ABCD的对角线AC,BD相交于O,E是AC上一点,过点A作AG⊥EB,垂足为G,AG交BD于点F. 求证:OE= OF.

答案： 证明：
∵四边形$ABCD$是正方形，
∴$OA = OB$，$\angle AOF=\angle BOE = 90^{\circ}$。
∵$AG\perp EB$，
∴$\angle FAO+\angle AEG = 90^{\circ}$。
∵在$Rt\triangle BOE$中，$\angle OBE+\angle AEG = 90^{\circ}$，
∴$\angle FAO=\angle OBE$。
在$\triangle AOF$和$\triangle BOE$中，
$\begin{cases}\angle AOF=\angle BOE\\OA = OB\\\angle FAO=\angle OBE\end{cases}$
∴$\triangle AOF\cong\triangle BOE(ASA)$。
∴$OE = OF$。

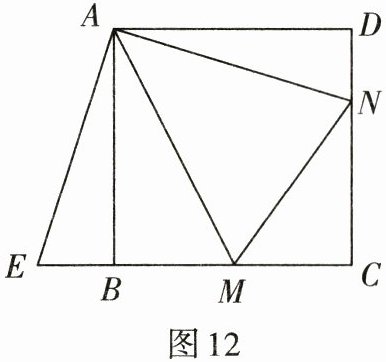
4. 如图12,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN= 45°,把△ADN绕点A顺时针旋转90°得到△ABE.
(1)求证:△AEM≌△ANM;
(2)若BM= 3,DN= 2,求正方形ABCD的边长.

答案：
(1)证明：
∵△ADN绕点A顺时针旋转90°得到△ABE，
∴AE=AN，∠BAE=∠DAN，BE=DN，
∵四边形ABCD是正方形，
∴∠BAD=90°，
∵∠MAN=45°，
∴∠BAM+∠DAN=45°，
∴∠BAM+∠BAE=45°，即∠EAM=45°，
∴∠EAM=∠NAM，
在△AEM和△ANM中，
$\left\{\begin{array}{l}AE=AN\\ \angle EAM=\angle NAM\\ AM=AM\end{array}\right.$，
∴△AEM≌△ANM(SAS)；
(2)解：设正方形ABCD的边长为x，则BC=CD=x，
∵BM=3，DN=2，
∴MC=BC-BM=x-3，CN=CD-DN=x-2，
∵△ADN绕点A顺时针旋转90°得到△ABE，
∴BE=DN=2，
∵△AEM≌△ANM，
∴EM=MN，
∵EM=BE+BM=2+3=5，
∴MN=5，
∵四边形ABCD是正方形，
∴∠C=90°，
在Rt△MCN中，根据勾股定理得：MC²+CN²=MN²，
即(x-3)²+(x-2)²=5²，
整理得：x²-5x-6=0，
解得：x₁=6，x₂=-1(不合题意，舍去)，
∴正方形ABCD的边长为6．