《2025年新课程课堂同步练习册九年级数学上册人教版》

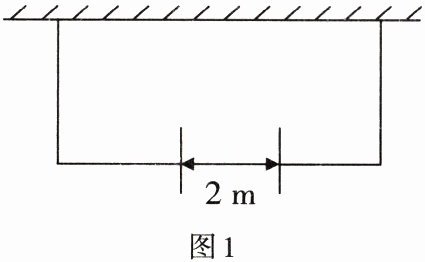
3. 如图1,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18 m,墙对面有一个2 m宽的门,另三边用竹篱笆围成,篱笆总长33 m,围成的长方形养鸡场除门之外四周不能有空隙.
(1)要围成养鸡场的面积为$150m^{2}$,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到$200m^{2}$? 请说明理由.

答案：
(1) 设垂直于墙的一边长为$x$米，则平行于墙的一边长为$(33 - 2x + 2)$米。
根据题意，有方程：
$x(33 - 2x + 2) = 150$
整理得：
$x^{2} - \frac{35}{2}x + 75 = 0$
通过求解一元二次方程，利用求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，其中$a = 1$，$b = -\frac{35}{2}$，$c = 75$，我们可以得到：
$x_{1} = 10, \quad x_{2} = 7.5$
当$x = 10$时，平行于墙的一边长为$33 - 2 × 10 + 2 = 15$（米），这符合题意；
当$x = 7.5$时，平行于墙的一边长为$33 - 2 × 7.5 + 2 = 20$（米），由于墙长只有18米，所以这不符合题意，应舍去。
答：养鸡场的长和宽分别为15米和10米。
(2) 不能达到$200m^{2}$，理由如下：
设垂直于墙的一边长为$x$米，则平行于墙的一边长为$(33 - 2x + 2)$米。
根据题意，有方程：
$x(33 - 2x + 2) = 200$
整理得：
$x^{2} - \frac{35}{2}x + 100 = 0$
接下来，我们计算判别式$\Delta$，其中$a = 1$，$b = -\frac{35}{2}$，$c = 100$：
$\Delta = b^{2} - 4ac = \left(-\frac{35}{2}\right)^{2} - 4 × 1 × 100 = \frac{1225}{4} - 400 = \frac{1225 - 1600}{4} = -\frac{375}{4} ＜ 0$
由于判别式$\Delta ＜ 0$，所以方程无解。
因此，围成养鸡场的面积不能达到$200m^{2}$。

4. 端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元. 经调查发现,零售单价每降低0.1元,每天可多卖出100只粽子. 为了使每天获取的利润更多,该店决定把零售单价下降m元($0＜m＜1$).
(1)零售单价下降m元后,该店平均每天可卖出$300 + 1000m$只粽子,每天获得的利润为$(1 - m)(300 + 1000m)$元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
解：由题意得$(1 - m)(300 + 1000m) = 420$
整理得$100m^2 - 70m + 12 = 0$
即$(10m - 3)(10m - 4) = 0$
解得$m_1 = 0.3$，$m_2 = 0.4$
当$m = 0.3$时，卖出粽子$300 + 1000×0.3 = 600$只
当$m = 0.4$时，卖出粽子$300 + 1000×0.4 = 700$只
因为$700 ＞ 600$，所以$m = 0.4$
答：当$m$定为$0.4$时，该店每天获取的利润是$420$元，并且卖出的粽子更多。

答案：
(1) $300 + 1000m$；$(1 - m)(300 + 1000m)$
(2) 解：由题意得$(1 - m)(300 + 1000m) = 420$
整理得$100m^2 - 70m + 12 = 0$
即$(10m - 3)(10m - 4) = 0$
解得$m_1 = 0.3$，$m_2 = 0.4$
当$m = 0.3$时，卖出粽子$300 + 1000×0.3 = 600$只
当$m = 0.4$时，卖出粽子$300 + 1000×0.4 = 700$只
因为$700 ＞ 600$，所以$m = 0.4$
答：当$m$定为$0.4$时，该店每天获取的利润是$420$元，并且卖出的粽子更多。