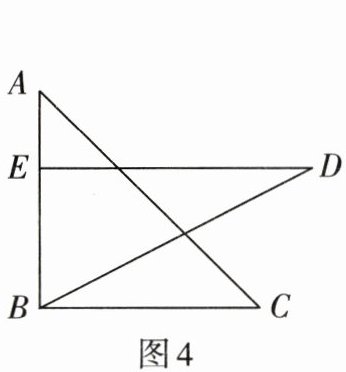
7. 把一副三角板按如图4放置,其中∠ABC= ∠DEB= 90°,∠A= 45°,∠D= 30°,斜边AC= BD= 10,若将三角板DEB绕点B逆时针旋转45°得到△D'E'B,则点A在△D'E'B的(
A.内部
B.外部
C.边上
D.以上都有可能
C
)
A.内部
B.外部
C.边上
D.以上都有可能
答案:
C
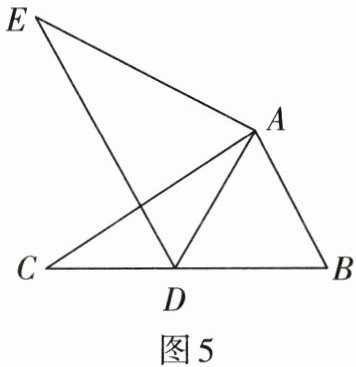
8. 如图5,在△ABC中,AB= 2,BC= 3.6,∠B= 60°,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为(
A.1.6
B.1.8
C.2
D.2.6
A
)
A.1.6
B.1.8
C.2
D.2.6
答案:
A
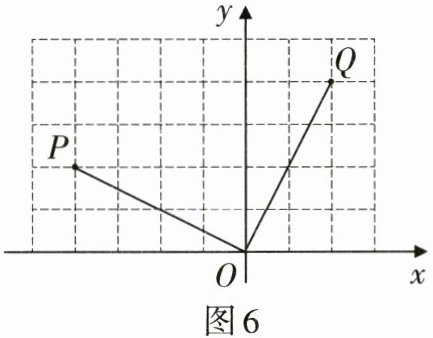
1. 如图6,在平面直角坐标系中,将点P(-4,2)绕原点O顺时针旋转90°,则其对应点Q的坐标为
(2,4)
.
答案:
$(2,4)$。
2. 如图7,将△ABC绕点C按顺时针方向旋转至△A'B'C,使点A'落在BC的延长线上. 已知∠A= 27°,∠B= 40°,则∠ACB'=

46
度.
答案:
解:在△ABC中,∠A=27°,∠B=40°,
∠ACB=180°-∠A-∠B=180°-27°-40°=113°.
由旋转性质得:∠A'CB'=∠ACB=113°,
点A'在BC延长线上,∠ACA'=180°-∠ACB=180°-113°=67°.
∠ACB'=∠A'CB'-∠ACA'=113°-67°=46°.
46
∠ACB=180°-∠A-∠B=180°-27°-40°=113°.
由旋转性质得:∠A'CB'=∠ACB=113°,
点A'在BC延长线上,∠ACA'=180°-∠ACB=180°-113°=67°.
∠ACB'=∠A'CB'-∠ACA'=113°-67°=46°.
46
3. 如图8,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF. 若AB= 3,AC= 2,且α+β= ∠B,则EF=

$\sqrt{13}$
.
答案:
解:在Rt△ABC中,∠C=90°,AB=3,AC=2,
∴∠B+∠BAC=90°,
由旋转的性质得:AE=AB=3,AF=AC=2,
∵α+β=∠B,
∴∠EAF=∠BAC+α+β=∠BAC+∠B=90°,
∴△EAF是直角三角形,
∴EF=$\sqrt{AE^{2}+AF^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$。
故答案为:$\sqrt{13}$。
∴∠B+∠BAC=90°,
由旋转的性质得:AE=AB=3,AF=AC=2,
∵α+β=∠B,
∴∠EAF=∠BAC+α+β=∠BAC+∠B=90°,
∴△EAF是直角三角形,
∴EF=$\sqrt{AE^{2}+AF^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$。
故答案为:$\sqrt{13}$。
4. 已知点A(a,1)与点B(-4,b)关于原点对称,则a-b的值为
5
.
答案:
解:
∵点A(a,1)与点B(-4,b)关于原点对称,
∴a=4,b=-1,
∴a-b=4-(-1)=5.
5
∵点A(a,1)与点B(-4,b)关于原点对称,
∴a=4,b=-1,
∴a-b=4-(-1)=5.
5
查看更多完整答案,请扫码查看


