《2025年新课程课堂同步练习册九年级数学上册华师大版》

1. 下列各组长度的线段,成比例线段的是( )

A.3 cm,6 cm,7 cm,9 cm
B.1.1 m,1.2 m,1.3 m,1.4 m
C.20 m,40 m,60 m,80 m
D.0.3 cm,0.6 cm,0.9 cm,1.8 cm

答案： 解：A. 将各线段长度从小到大排列：3cm，6cm，7cm，9cm
3×9=27，6×7=42，27≠42，不成比例。
B. 将各线段长度从小到大排列：1.1m，1.2m，1.3m，1.4m
1.1×1.4=1.54，1.2×1.3=1.56，1.54≠1.56，不成比例。
C. 将各线段长度从小到大排列：20m，40m，60m，80m
20×80=1600，40×60=2400，1600≠2400，不成比例。
D. 将各线段长度从小到大排列：0.3cm，0.6cm，0.9cm，1.8cm
0.3×1.8=0.54，0.6×0.9=0.54，0.54=0.54，成比例。
答案：D

2. 如图1,直线$l_1 // l_2 // l_3$,直线AC和DF被$l_1,l_2,l_3$所截,AB= 5,BC= 6,EF= 4,则DE的长为( )


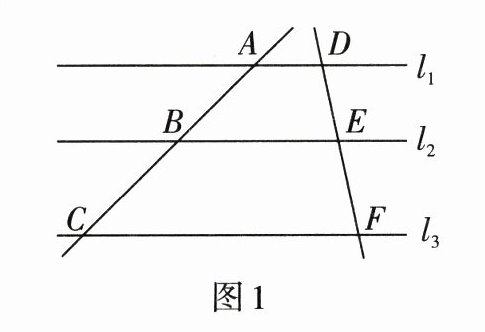
A.2
B.3
C.4
D.$\frac{10}{3}$

答案： 【解析】：
本题主要考查平行线分线段成比例定理。
由于直线$l_1$、$l_2$、$l_3$相互平行，根据平行线分线段成比例定理，我们有：
$\frac{AB}{BC} = \frac{DE}{EF}$
代入已知条件$AB=5$，$BC=6$，$EF=4$，我们得到：
$\frac{5}{6} = \frac{DE}{4}$
通过交叉相乘，我们得到：
$5 × 4 = 6 × DE$
$20 = 6DE$
$DE = \frac{20}{6}$
$DE = \frac{10}{3}$
【答案】：
D. $\frac{10}{3}$。

3. 如图2,将$\triangle ABC$沿DE翻折,折痕$DE // BC$,若$\frac{AD}{BD}= \frac{1}{2}$,BC= 6,则DE的长等于( )


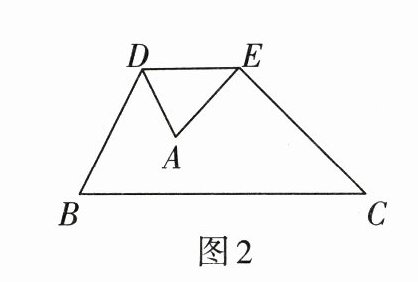
A.1.8
B.2
C.2.5
D.3

答案： 解：
∵DE//BC，
∴△ADE∽△ABC。
∵$\frac{AD}{BD} = \frac{1}{2}$，
∴设AD = k，BD = 2k，则AB = AD + BD = 3k。
∴$\frac{AD}{AB} = \frac{k}{3k} = \frac{1}{3}$。
∵△ADE∽△ABC，
∴$\frac{DE}{BC} = \frac{AD}{AB} = \frac{1}{3}$。
∵BC = 6，
∴$\frac{DE}{6} = \frac{1}{3}$，解得DE = 2。
答案：B

4. 如图3,D,E两点分别在AC,AB上,且DE与BC不平行,那么添加下列一个条件后,仍无法判定$\triangle ADE \sim \triangle ABC$的是( )


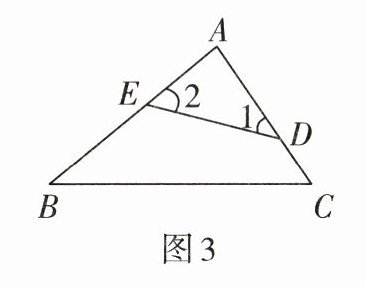
A.$\frac{AE}{AC}= \frac{AD}{AB}$
B.$\frac{AE}{AC}= \frac{ED}{BC}$
C.$\angle 1= \angle B$
D.$\angle 2= \angle C$

答案： 【解析】：
本题主要考察相似三角形的判定条件。
相似三角形有以下几种判定方式：
1. 两角对应相等的三角形为相似三角形。
2. 两边对应成比例且夹角相等的三角形为相似三角形。
3. 三边对应成比例的三角形为相似三角形。
对于选项A：若$\frac{AE}{AC} = \frac{AD}{AB}$，且$\angle A = \angle A$（公共角），则根据两边对应成比例且夹角相等的三角形判定，$\triangle ADE \sim \triangle ABC$。
对于选项B：若$\frac{AE}{AC} = \frac{ED}{BC}$，仅给出了两边对应成比例，但并未给出夹角相等的信息，因此不能判定$\triangle ADE \sim \triangle ABC$。
对于选项C：若$\angle 1 = \angle B$，且$\angle A = \angle A$（公共角），则根据两角对应相等的三角形判定，$\triangle ADE \sim \triangle ABC$。
对于选项D：若$\angle 2 = \angle C$，且$\angle A = \angle A$（公共角），同样根据两角对应相等的三角形判定，$\triangle ADE \sim \triangle ABC$。
综上所述，只有选项B添加后仍无法判定$\triangle ADE \sim \triangle ABC$。
【答案】：
B

5. 如图4,在测量凹透镜焦距时,用一束平行于凹透镜主光轴的光线,射向嵌入挡板中直径为d的凹透镜上,在光屏上形成一个直径为m的圆形光斑,测得光屏到凹透镜的距离为n. 若凹透镜的焦距为f,则下列结论正确的是( )


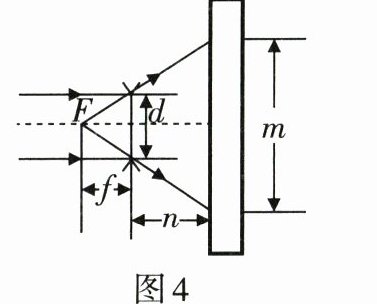
A.$\frac{f}{n}= \frac{d}{m}$
B.$\frac{f}{n+f}= \frac{d}{m}$
C.$\frac{f}{n-f}= \frac{d}{m}$
D.$f= \frac{nd}{m+d}$

答案： 解：根据凹透镜对光线的发散作用，平行于主光轴的光线经凹透镜折射后，其反向延长线过焦点。设凹透镜光心为O，焦点为F，焦距OF=f。平行光线经凹透镜折射后形成发散光束，在光屏上形成直径为m的光斑，光屏到凹透镜距离为n。
过焦点F作平行于主光轴的辅助线，可得两个相似三角形：一个以凹透镜直径d为底边、焦距f为高；另一个以光斑直径m为底边、（f+n）为高（因光屏在凹透镜另一侧，距离为n，故总距离为f+n）。
由相似三角形对应边成比例得：$\frac{d}{m}=\frac{f}{f+n}$，即$\frac{f}{n+f}=\frac{d}{m}$。
答案：B

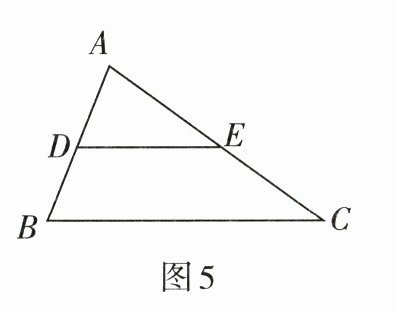
6. 如图5,在$\triangle ABC$中,点D,E分别是AB,AC的中点,若$\triangle ADE的面积是3\ \text{cm}^2$,则四边形BDEC的面积为( )


A.$12\ \text{cm}^2$
B.$9\ \text{cm}^2$
C.$6\ \text{cm}^2$
D.$3\ \text{cm}^2$

答案： 解：
∵点D，E分别是AB，AC的中点，
∴DE是△ABC的中位线，
∴DE//BC，DE=1/2BC，
∴△ADE∽△ABC，相似比为1:2，
∴S△ADE/S△ABC=(1/2)²=1/4，
∵S△ADE=3 cm²，
∴3/S△ABC=1/4，
∴S△ABC=12 cm²，
∴S四边形BDEC=S△ABC - S△ADE=12 - 3=9 cm²。
答案：B