《2025年新课程课堂同步练习册九年级数学上册华师大版》

1. $\tan60^{\circ}$的值等于( )

A.$\frac{\sqrt{3}}{3}$
B.$\frac{\sqrt{2}}{2}$
C.$\sqrt{3}$
D.1

答案： 解：在直角三角形中，$\tan\theta=\frac{对边}{邻边}$。对于$60^{\circ}$角的直角三角形，设$30^{\circ}$所对直角边为$a$，则斜边为$2a$，$60^{\circ}$所对直角边为$\sqrt{(2a)^2 - a^2}=\sqrt{3}a$。所以$\tan60^{\circ}=\frac{\sqrt{3}a}{a}=\sqrt{3}$。
答案：C

2. 已知$\angle A$是锐角,且$\cos A= \frac{1}{2}$,则$\angle A$的度数为( )

A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$

答案： 解：
∵∠A是锐角，cosA=1/2，
∴∠A=60°。
答案：C

3. 某斜坡的坡度$i= 1:\sqrt{3}$,则该斜坡的坡角为( )

A.$75^{\circ}$
B.$60^{\circ}$
C.$45^{\circ}$
D.$30^{\circ}$

答案： 解：设坡角为α，坡度i=1:√3，即tanα=1/√3=√3/3。
∵tan30°=√3/3，
∴α=30°。
答案：D

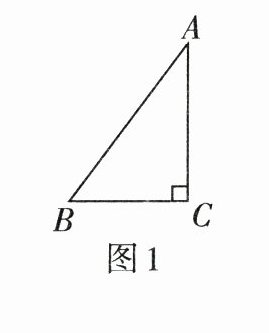
4. 如图1,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$AB= 5$,$AC= 4$,下列三角函数表示正确的是( )


A.$\sin A= \frac{4}{5}$
B.$\cos A= \frac{4}{5}$
C.$\tan A= \frac{4}{3}$
D.$\tan B= \frac{4}{5}$

答案： B

5. 在$\text{Rt}\triangle ABC$中,$\angle C= 90^{\circ}$,$\tan A= \frac{5}{12}$,则$\sin B$的值为( )

A.$\frac{5}{13}$
B.$\frac{12}{13}$
C.$\frac{13}{5}$
D.$\frac{13}{12}$

答案： 解：在Rt△ABC中，∠C=90°，tanA=BC/AC=5/12。
设BC=5k，AC=12k（k＞0），
由勾股定理得AB=√(AC²+BC²)=√[(12k)²+(5k)²]=13k，
∠A+∠B=90°，则sinB=sin(90°-∠A)=cosA=AC/AB=12k/13k=12/13。
答案：B

6. 在$\text{Rt}\triangle ABC$中,$\angle C= 90^{\circ}$,$\cos A= \frac{1}{2}$,$AC= 2\sqrt{3}$,则$BC$的值为( )

A.2
B.4
C.$4\sqrt{3}$
D.6

答案： 解：在Rt△ABC中，∠C=90°，
∵cosA=AC/AB=1/2，AC=2√3，
∴2√3/AB=1/2，解得AB=4√3，
由勾股定理得，BC=√(AB²-AC²)=√[(4√3)²-(2√3)²]=√(48-12)=√36=6。
答案：D

7. 如图2,$P是\angle \alpha的边OA$上一点,且点$P的坐标为(3,4)$,则$\cos\alpha=$( )


A.$\frac{3}{5}$
B.$\frac{4}{5}$
C.$\frac{3}{4}$
D.$\frac{4}{3}$

答案： 解：过点P作PB⊥x轴于点B，
∵点P坐标为(3,4)，
∴OB=3，PB=4，
在Rt△POB中，OP=$\sqrt{OB^2+PB^2}=\sqrt{3^2+4^2}=5$，
$\cos\alpha=\frac{OB}{OP}=\frac{3}{5}$，
答案：A.

8. 如图3,小雅家(图中点$O$处)门前有一条东西走向的公路,经测得有一水塔(图中点$A$处)在家北偏东60度500 m处,那么水塔所在的位置到公路的距离$AB$是( )


A.$250\sqrt{3}\ \text{m}$
B.250 m
C.$\frac{500}{3}\sqrt{3}\ \text{m}$
D.$250\sqrt{2}\ \text{m}$

答案： B