《2025年新课程课堂同步练习册九年级数学上册华师大版》

4. 某商店经销一批季节性小家电,每件成本40元.试销中发现这种小家电每天的销售量$p$(件)与每件的销售价$x$(元)满足关系：$p= 700-10x$.若该商店每天销售这种小家电要获得2000元的利润,那么每件的售价应定为多少元？每天要售出多少件？

答案： 解：根据题意，每件利润为$(x - 40)$元，销售量为$p = 700 - 10x$件，总利润为$2000$元，可得方程：
$(x - 40)(700 - 10x) = 2000$
展开并整理得：$x^2 - 110x + 3000 = 0$
因式分解得：$(x - 50)(x - 60) = 0$
解得：$x_1 = 50$，$x_2 = 60$
当$x = 50$时，$p = 700 - 10×50 = 200$（件）
当$x = 60$时，$p = 700 - 10×60 = 100$（件）
答：每件售价应定为50元，每天售出200件；或每件售价定为60元，每天售出100件。

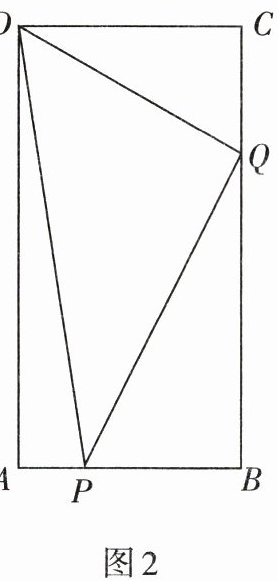
5. 如图2,在矩形$ABCD$中,$AB= 6\ \text{cm},BC= 12\ \text{cm}$,点$P从点A沿边AB向点B$以1 cm/s的速度移动；同时,点$Q从点B沿边BC向点C$以2 cm/s的速度移动,设运动的时间为$t$秒,有一点到终点运动即停止.问：是否存在这样的时刻,使$S_{\triangle DPQ}= 28\ \text{cm}^2$？若存在,请求出$t$的值；若不存在,请说明理由.

答案： 解：由题意得，运动时间为$t$秒，$AP = t\ \text{cm}$，$BQ = 2t\ \text{cm}$，其中$0 \leq t \leq 6$（因为$P$到$B$停止，$AB=6\ \text{cm}$，速度$1\ \text{cm/s}$）。
则$PB = AB - AP = 6 - t\ \text{cm}$，$QC = BC - BQ = 12 - 2t\ \text{cm}$。
矩形$ABCD$面积为$AB × BC = 6 × 12 = 72\ \text{cm}^2$。
$S_{\triangle APD} = \frac{1}{2} × AP × AD = \frac{1}{2} × t × 12 = 6t\ \text{cm}^2$，
$S_{\triangle PBQ} = \frac{1}{2} × PB × BQ = \frac{1}{2} × (6 - t) × 2t = t(6 - t)\ \text{cm}^2$，
$S_{\triangle QCD} = \frac{1}{2} × QC × CD = \frac{1}{2} × (12 - 2t) × 6 = 3(12 - 2t) = 36 - 6t\ \text{cm}^2$。
因为$S_{\triangle DPQ} = S_{矩形ABCD} - S_{\triangle APD} - S_{\triangle PBQ} - S_{\triangle QCD}$，
所以$28 = 72 - 6t - t(6 - t) - (36 - 6t)$，
化简得：$28 = 72 - 6t - 6t + t^2 - 36 + 6t$，
$28 = t^2 - 6t + 36$，
$t^2 - 6t + 8 = 0$，
$(t - 2)(t - 4) = 0$，
解得$t_1 = 2$，$t_2 = 4$，均在$0 \leq t \leq 6$范围内。
答：存在时刻$t = 2\ \text{秒}$或$t = 4\ \text{秒}$，使$S_{\triangle DPQ}= 28\ \text{cm}^2$。