《2025年新课程课堂同步练习册九年级数学上册华师大版》

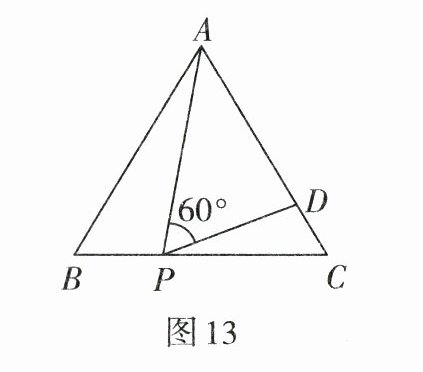
1. 如图13,等边$\triangle ABC$的边长为3,点P为BC上一点,且BP= 1,点D为AC上一点,若$\angle APD= 60^\circ$,求CD的长.

答案： 解：
∵△ABC是等边三角形，
∴∠B=∠C=60°，AB=BC=AC=3。
∵BP=1，
∴PC=BC-BP=3-1=2。
设CD=x，则AD=AC-CD=3-x。
∵∠APC=∠APD+∠DPC=60°+∠DPC，
且∠APC=∠B+∠BAP=60°+∠BAP，
∴∠BAP=∠DPC。
∵∠B=∠C=60°，
∴△ABP∽△PCD。
∴$\frac{AB}{PC}=\frac{BP}{CD}$，即$\frac{3}{2}=\frac{1}{x}$。
解得$x=\frac{2}{3}$。
∴CD的长为$\frac{2}{3}$。

2. 在图14的方格纸中,$\triangle OAB$的顶点坐标分别为O(0,0),A(-2,-1),B(-1,-3),P(a,b)是$\triangle AOB$的边AB上一点.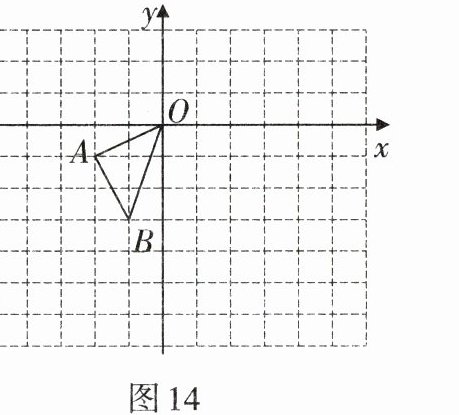
(1)以原点O为位似中心,在y轴的左侧画出$\triangle OAB的一个位似图形\triangle OA_1B_1$,使它与$\triangle OAB$的相似比为2:1,并分别写出点A,P的对应点$A_1,P_1$的坐标;
(2)画出将$\triangle OA_1B_1$向右平移5个单位后的$\triangle OA_2B_2$,并写出点$A_2,P_2$的坐标;
(3)判断$\triangle OAB与\triangle OA_2B_2$能否是关于某一点M为位似中心的位似图形,若是,请在图中标出位似中心M,并写出点M的坐标.

答案： 【解析】：
(1) 根据位似图形的性质，我们知道如果两个图形是位似的，那么它们的对应点之间的连线都会经过同一个点（位似中心），并且对应点到位似中心的距离之比是恒定的。本题中，位似中心是原点O，相似比为2:1。因此，点A和点P的对应点$A_1$和$P_1$的坐标可以通过将原坐标乘以-2来得到（因为在y轴的左侧，所以乘以-2）。
点A的坐标是$(-2, -1)$，所以$A_1$的坐标是$(-2 × -2, -1 × -2) = (4, 2)$的相反数，即$(-4, -2)$。
设点P的坐标为$(a, b)$，则$P_1$的坐标为$(-2a, -2b)$。
(2) 平移是图形在平面上按某一方向移动一定的距离，而不改变其形状和大小。本题中，需要将$\triangle OA_1B_1$向右平移5个单位。因此，点$A_1$和点$P_1$的新坐标可以通过将原坐标的x值加5来得到。
点$A_1$的坐标是$(-4, -2)$，所以$A_2$的坐标是$(-4 + 5, -2) = (1, -2)$。
点$P_1$的坐标是$(-2a, -2b)$，所以$P_2$的坐标是$(-2a + 5, -2b)$。
(3) 如果$\triangle OAB$与$\triangle OA_2B_2$是关于某一点M为位似中心的位似图形，那么对应点之间的连线应该会交于这一点。我们可以通过找到两组对应点的连线的交点来确定这一点。在本题中，可以通过找到线段OA和线段$OA_2$的中点，然后连接这两个中点，这条连线与x轴的交点即为位似中心M。通过计算可以得到M的坐标为$(\frac{5}{2}, 0)$，
【答案】：
(1) 点$A_1$的坐标为$(-4, -2)$，点$P_1$的坐标为$(-2a, -2b)$；
(2) 点$A_2$的坐标为$(1, -2)$，点$P_2$的坐标为$(5-2a, -2b)$；
(3)$\triangle OAB$与$\triangle OA_2B_2$是关于点$M(\frac{5}{2}, 0)$为位似中心的位似图形。