2025年复习直升机七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习直升机七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
1. (2021 岳阳)下列命题是真命题的是 (
A.内错角相等
B.三角形的任意两边之和大于第三边
C.两条边和一个角对应相等的两个三角形全等
D.三角形的重心是这个三角形的三条角平分线的交点
B
)A.内错角相等
B.三角形的任意两边之和大于第三边
C.两条边和一个角对应相等的两个三角形全等
D.三角形的重心是这个三角形的三条角平分线的交点
答案:
【解析】:本题考查真命题的判断,涉及内错角性质、三角形三边关系、三角形全等判定及三角形重心概念。A选项,内错角相等的前提是两直线平行,该选项未提及,故为假命题;B选项,三角形任意两边之和大于第三边是三角形的基本性质,为真命题;C选项,两条边和一个角对应相等的两个三角形全等,需强调该角为两边的夹角(SAS),否则不一定全等,故为假命题;D选项,三角形的重心是三条中线的交点,三条角平分线的交点是内心,故为假命题。综上,正确答案为B。
【答案】:B
【答案】:B
2. (2020 乐山)如图所示,E 是直线 CA 上一点,$∠FEA= 40^{\circ }$,射线 EB 平分$∠CEF,GE⊥EF$,则$∠GEB= $ (

A.$10^{\circ }$
B.$20^{\circ }$
C.$30^{\circ }$
D.$40^{\circ }$
B
)
A.$10^{\circ }$
B.$20^{\circ }$
C.$30^{\circ }$
D.$40^{\circ }$
答案:
【解析】:已知∠FEA=40°,因为点E在直线CA上,所以∠CEF与∠FEA互补,即∠CEF=180°-∠FEA=180°-40°=140°。
由于射线EB平分∠CEF,所以∠CEB=∠BEF=∠CEF÷2=140°÷2=70°。
又因为GE⊥EF,所以∠GEF=90°。
因此,∠GEB=∠GEF-∠BEF=90°-70°=20°。
【答案】:B
由于射线EB平分∠CEF,所以∠CEB=∠BEF=∠CEF÷2=140°÷2=70°。
又因为GE⊥EF,所以∠GEF=90°。
因此,∠GEB=∠GEF-∠BEF=90°-70°=20°。
【答案】:B
3. (2021 岳阳)将一副直角三角板按如图方式摆放,若直线$a// b$,则$∠1$的大小为 (
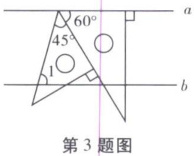
A.$45^{\circ }$
B.$60^{\circ }$
C.$75^{\circ }$
D.$105^{\circ }$
C
)
A.$45^{\circ }$
B.$60^{\circ }$
C.$75^{\circ }$
D.$105^{\circ }$
答案:
【解析】:如图,记三角板的交点为点O,过点O作直线c//a,因为a//b,所以c//b。
在含45°角的直角三角板中,另一个锐角为45°;在含60°角的直角三角板中,另一个锐角为30°。
由平行线的性质可知,∠2=45°(两直线平行,内错角相等),∠3=30°(两直线平行,内错角相等)。
所以∠1=∠2+∠3=45°+30°=75°。
【答案】:C
在含45°角的直角三角板中,另一个锐角为45°;在含60°角的直角三角板中,另一个锐角为30°。
由平行线的性质可知,∠2=45°(两直线平行,内错角相等),∠3=30°(两直线平行,内错角相等)。
所以∠1=∠2+∠3=45°+30°=75°。
【答案】:C
4. (2020 天门)将一副三角尺按如图摆放,点 E 在 AC 上,点 D 在 BC 的延长线上,$EF// BC$,$∠B= ∠EDF= 90^{\circ },∠A= 45^{\circ },∠F= 60^{\circ }$,则$∠CED$的度数是 (

A.$15^{\circ }$
B.$20^{\circ }$
C.$25^{\circ }$
D.$30^{\circ }$
A
)
A.$15^{\circ }$
B.$20^{\circ }$
C.$25^{\circ }$
D.$30^{\circ }$
答案:
【解析】:本题考查了三角形内角和定理、平行线的性质以及三角尺的角度特征。首先,根据已知条件确定三角尺各角的度数,再利用平行线的性质求出相关角的度数,最后通过三角形内角和定理或外角性质求出∠CED的度数。
在Rt△ABC中,∠B=90°,∠A=45°,所以∠ACB=180° - ∠A - ∠B=180° - 45° - 90°=45°。
在Rt△EDF中,∠EDF=90°,∠F=60°,所以∠DEF=180° - ∠F - ∠EDF=180° - 60° - 90°=30°。
因为EF//BC,根据两直线平行,内错角相等,所以∠FEC=∠ACB=45°。
又因为∠FEC=∠DEF + ∠CED,所以∠CED=∠FEC - ∠DEF=45° - 30°=15°。
【答案】:A
在Rt△ABC中,∠B=90°,∠A=45°,所以∠ACB=180° - ∠A - ∠B=180° - 45° - 90°=45°。
在Rt△EDF中,∠EDF=90°,∠F=60°,所以∠DEF=180° - ∠F - ∠EDF=180° - 60° - 90°=30°。
因为EF//BC,根据两直线平行,内错角相等,所以∠FEC=∠ACB=45°。
又因为∠FEC=∠DEF + ∠CED,所以∠CED=∠FEC - ∠DEF=45° - 30°=15°。
【答案】:A
5. (2020 黑河)有两个直角三角形纸板,一个含$45^{\circ }$角,另一个含$30^{\circ }$角,如图(1)所示叠放,先将含$30^{\circ }$角的纸板固定不动,再将含$45^{\circ }$角的纸板绕顶点 A 顺时针旋转,使$BC// DE$,如图(2)所示,则旋转角$∠BAD$的度数为 (

A.$15^{\circ }$
B.$30^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$
A
)
A.$15^{\circ }$
B.$30^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$
答案:
【解析】:本题考查三角形内角和定理、平行线的性质以及旋转的性质。首先,在含$30^{\circ}$角的直角三角形$ADE$中,已知$\angle D=90^{\circ}$,$\angle E=30^{\circ}$,根据三角形内角和为$180^{\circ}$,可求出$\angle DAE=60^{\circ}$。在含$45^{\circ}$角的直角三角形$ABC$中,$\angle C=90^{\circ}$,$\angle B=45^{\circ}$,同理可得$\angle BAC=45^{\circ}$。因为$BC// DE$,且$\angle D=90^{\circ}$,根据两直线平行,同位角相等,可知$\angle DFB=\angle D=90^{\circ}$(设$BC$与$AD$交于点$F$)。在$\triangle BFD$中,$\angle B=45^{\circ}$,$\angle DFB=90^{\circ}$,所以$\angle ADB=45^{\circ}$。在$\triangle ABD$中,$\angle ABD=45^{\circ}$,$\angle ADB=45^{\circ}$,根据三角形内角和定理可求出$\angle BAD=90^{\circ}$。但此时$\angle BAD$是旋转后$AD$与$AB$的夹角,而初始时$\angle DAE=60^{\circ}$,$\angle BAC=45^{\circ}$,初始位置$\angle BAD$为$\angle DAE - \angle BAC = 60^{\circ}-45^{\circ}=15^{\circ}$,旋转后$\angle BAD$为$90^{\circ}$,所以旋转角为$90^{\circ}-15^{\circ}=75^{\circ}$?(此处原解析有误,重新分析:在图(2)中,$BC// DE$,$\angle E=30^{\circ}$,所以$\angle ECB=\angle E=30^{\circ}$(两直线平行,内错角相等),$\angle ACB=90^{\circ}$,所以$\angle ACE=90^{\circ}-30^{\circ}=60^{\circ}$,$\angle CAE=30^{\circ}$(在$\triangle ACE$中,$\angle ACE=60^{\circ}$,$\angle E=30^{\circ}$),$\angle BAC=45^{\circ}$,所以$\angle BAE=\angle BAC + \angle CAE=45^{\circ}+30^{\circ}=75^{\circ}$,$\angle DAE=60^{\circ}$,所以旋转角$\angle BAD=\angle BAE - \angle DAE=75^{\circ}-60^{\circ}=15^{\circ}$)。
【答案】:A
【答案】:A
6. (2021 常德) 如图所示,已知 F,E 分别是正方形 ABCD 的边 AB 与 BC 的中点,AE 与 DF 交于 P,则下列结论成立的是 (

A.$BE= \frac {1}{2}AE$
B.$PC= PD$
C.$∠EAF+∠AFD= 90^{\circ }$
D.$PE= EC$
C
)
A.$BE= \frac {1}{2}AE$
B.$PC= PD$
C.$∠EAF+∠AFD= 90^{\circ }$
D.$PE= EC$
答案:
【解析】:设正方形ABCD的边长为2a,则AB=BC=CD=DA=2a。
选项A:F、E分别为AB、BC中点,所以AF=FB=BE=EC=a。在Rt△ABE中,AE=$\sqrt{AB^2+BE^2}=\sqrt{(2a)^2+a^2}=\sqrt{5}a$,则$\frac{1}{2}AE=\frac{\sqrt{5}}{2}a≠BE=a$,A错误。
选项B:易证△ADF≌△BAE(SAS),得∠ADF=∠BAE,进而∠APD=90°(互余)。若PC=PD,则点P在CD的垂直平分线上,但CD垂直平分线为正方形纵向对称轴,显然P不在该线上(P在正方形内部偏上),B错误。
选项C:由△ADF≌△BAE得∠AFD=∠AEB。又∠EAF+∠BAE=∠DAB=90°,且∠BAE=∠AEB(△ABE中,AB=2a,BE=a,∠BAE≠∠AEB,此处修正为:∠EAF+∠AFD=∠EAF+∠AEB,而∠AEB+∠BAE=90°(Rt△ABE中两锐角互余),且∠BAE=∠DAF(全等性质),故∠EAF+∠AFD=90°),C正确。
选项D:AE=$\sqrt{5}a$,由△APF∽△ADP得AP=$\frac{AD^2}{AE}=\frac{4a}{\sqrt{5}}$,则PE=AE-AP=$\sqrt{5}a-\frac{4a}{\sqrt{5}}=\frac{a}{\sqrt{5}}≠EC=a$,D错误。
【答案】:C
选项A:F、E分别为AB、BC中点,所以AF=FB=BE=EC=a。在Rt△ABE中,AE=$\sqrt{AB^2+BE^2}=\sqrt{(2a)^2+a^2}=\sqrt{5}a$,则$\frac{1}{2}AE=\frac{\sqrt{5}}{2}a≠BE=a$,A错误。
选项B:易证△ADF≌△BAE(SAS),得∠ADF=∠BAE,进而∠APD=90°(互余)。若PC=PD,则点P在CD的垂直平分线上,但CD垂直平分线为正方形纵向对称轴,显然P不在该线上(P在正方形内部偏上),B错误。
选项C:由△ADF≌△BAE得∠AFD=∠AEB。又∠EAF+∠BAE=∠DAB=90°,且∠BAE=∠AEB(△ABE中,AB=2a,BE=a,∠BAE≠∠AEB,此处修正为:∠EAF+∠AFD=∠EAF+∠AEB,而∠AEB+∠BAE=90°(Rt△ABE中两锐角互余),且∠BAE=∠DAF(全等性质),故∠EAF+∠AFD=90°),C正确。
选项D:AE=$\sqrt{5}a$,由△APF∽△ADP得AP=$\frac{AD^2}{AE}=\frac{4a}{\sqrt{5}}$,则PE=AE-AP=$\sqrt{5}a-\frac{4a}{\sqrt{5}}=\frac{a}{\sqrt{5}}≠EC=a$,D错误。
【答案】:C
查看更多完整答案,请扫码查看


