《2025年复习直升机七年级数学北师大版》

1. 计算$a\cdot a\cdot a^{x}= a^{12}$,则 x 等于 (A)
A.10
B.4
C.8
D.9

答案： 【解析】：根据同底数幂相乘，底数不变，指数相加。左边式子中$a\cdot a\cdot a^{x}$，前两个$a$的指数都为1，所以指数相加可得$1 + 1 + x$。已知等式右边为$a^{12}$，则有$1 + 1 + x = 12$，即$2 + x = 12$，解得$x = 10$。
【答案】：A

2. 下列运算正确的是 (B)
A.$x^{2}+x^{3}= x^{5}$
B.$(-2a^{2})^{3}= -8a^{6}$
C.$x^{2}\cdot x^{3}= x^{6}$
D.$x^{6}÷x^{2}= x^{3}$

答案： 【解析】：本题考查整式的运算，涉及合并同类项、幂的乘方与积的乘方、同底数幂的乘法和除法。
选项A：$x^2$与$x^3$不是同类项，不能合并，所以A错误。
选项B：根据积的乘方和幂的乘方，$(-2a^2)^3=(-2)^3\cdot (a^2)^3=-8a^6$，所以B正确。
选项C：同底数幂相乘，底数不变，指数相加，$x^2\cdot x^3=x^{2+3}=x^5$，所以C错误。
选项D：同底数幂相除，底数不变，指数相减，$x^6÷x^2=x^{6-2}=x^4$，所以D错误。
【答案】：B

3. 计算$-(a-b)^{3}(b-a)^{2}$的结果为 (D)
A.$(b+a)^{5}$
B.$-(b+a)^{5}$
C.$(a-b)^{5}$
D.$(b-a)^{5}$

答案： 【解析】：本题考查整式的运算，主要涉及同底数幂的乘法以及幂的符号变化。首先，观察到式子中底数分别为$(a - b)^3$和$(b - a)^2$，需要将它们化为同底数幂。因为$(b - a)^2 = [-(a - b)]^2 = (a - b)^2$（负数的偶次幂是正数），所以原式可变形为$-(a - b)^3 \cdot (a - b)^2$。根据同底数幂相乘，底数不变，指数相加，可得$-(a - b)^{3 + 2} = -(a - b)^5$。又因为$-(a - b)^5 = (b - a)^5$（提出负号后，$(a - b)^5$变为$-(b - a)^5$，所以$-(a - b)^5 = (b - a)^5$）。
【答案】：D

4. 下列运算正确的是 (C)
A.$a^{2}\cdot a^{3}= a^{6}$
B.$(-a^{2})^{3}= -a^{5}$
C.$a^{10}÷a^{9}= a(a≠0)$
D.$(-bc)^{4}÷(-bc)^{2}= -b^{2}c^{2}$

答案： 【解析】：本题考查整式的运算，涉及同底数幂的乘法、幂的乘方、同底数幂的除法以及积的乘方。
选项A：根据同底数幂相乘，底数不变，指数相加，$a^{2}\cdot a^{3}=a^{2+3}=a^{5}$，而不是$a^{6}$，所以A错误。
选项B：根据幂的乘方，底数不变，指数相乘，$(-a^{2})^{3}=(-1)^3\cdot (a^{2})^{3}=-a^{6}$，而不是$-a^{5}$，所以B错误。
选项C：根据同底数幂相除，底数不变，指数相减，$a^{10}÷a^{9}=a^{10-9}=a(a≠0)$，所以C正确。
选项D：先算同底数幂相除，$(-bc)^{4}÷(-bc)^{2}=(-bc)^{4-2}=(-bc)^{2}=b^{2}c^{2}$，而不是$-b^{2}c^{2}$，所以D错误。
【答案】：C

5. 下列运算错误的是 (D)
A.$(-2a^{2}b)^{3}= -8a^{6}b^{3}$
B.$(x^{2}y^{4})^{3}= x^{6}y^{12}$
C.$(-x)^{2}\cdot (x^{3}y)^{2}= x^{8}y^{2}$
D.$(-ab)^{7}= -ab^{7}$

答案： 【解析】：本题考查整式的运算，涉及积的乘方、幂的乘方以及同底数幂的乘法。需要对每个选项逐一进行计算，判断其运算是否正确。
A选项：根据积的乘方，先把积中的每一个乘数分别乘方，再把所得的幂相乘。$(-2a^{2}b)^{3}=(-2)^3\cdot (a^{2})^3\cdot b^3=-8a^{6}b^{3}$，运算正确。
B选项：$(x^{2}y^{4})^{3}=(x^{2})^3\cdot (y^{4})^3=x^{6}y^{12}$，运算正确。
C选项：$(-x)^{2}\cdot (x^{3}y)^{2}=x^{2}\cdot x^{6}y^{2}=x^{8}y^{2}$（先算乘方，$(-x)^2=x^2$，$(x^3y)^2=(x^3)^2\cdot y^2=x^6y^2$，再算同底数幂相乘，底数不变指数相加），运算正确。
D选项：$(-ab)^{7}=(-1)^7\cdot a^7\cdot b^7=-a^{7}b^{7}$，而不是$-ab^{7}$，运算错误。
【答案】：D

6. 小明总结了以下结论:
①$a(b+c)= ab+ac$;
②$a(b-c)= ab-ac$;
③$(b-c)÷a= b÷a-c÷a(a≠0)$;
④$a÷(b+c)= a÷b+a÷c(a≠0)$.
其中一定成立的个数是 (C)
A.1
B.2
C.3
D.4

答案： 【解析】：本题考查整式运算中的乘法分配律及其逆运算。①式$a(b + c)=ab + ac$，这是乘法分配律，显然成立；②式$a(b - c)=ab - ac$，同样是乘法分配律的应用，成立；③式$(b - c)÷ a = b÷ a - c÷ a(a\neq0)$，可看作乘法分配律对除法的推广，当$a\neq0$时成立；④式$a÷(b + c)=a÷ b + a÷ c(a\neq0)$，除法没有分配律，例如当$a = 4$，$b = 1$，$c = 1$时，左边$=4÷(1 + 1)=2$，右边$=4÷1 + 4÷1=8$，左边≠右边，所以④不成立。综上，①②③成立，共3个。
【答案】：C

7. 下列运算不正确的是 (B)
A.$xy+x-y-1= (x-1)(y+1)$
B.$x^{2}+y^{2}+z^{2}+xy+yz+zx= \frac {1}{2}(x+y+z)^{2}$
C.$(x+y)(x^{2}-xy+y^{2})= x^{3}+y^{3}$
D.$(x-y)^{3}= x^{3}-3x^{2}y+3xy^{2}-y^{3}$

答案： 【解析】：本题考查整式的运算，包括因式分解、乘法公式及多项式乘法。需要对每个选项逐一分析判断其正确性。
选项A：对右边$(x - 1)(y + 1)$展开，$x\cdot y + x\cdot1 - 1\cdot y - 1\cdot1 = xy + x - y - 1$，与左边相等，所以A正确。
选项B：计算$\frac{1}{2}(x + y + z)^2$，先展开$(x + y + z)^2 = x^2 + y^2 + z^2 + 2xy + 2yz + 2zx$，则$\frac{1}{2}(x + y + z)^2 = \frac{1}{2}x^2 + \frac{1}{2}y^2 + \frac{1}{2}z^2 + xy + yz + zx$，与左边$x^2 + y^2 + z^2 + xy + yz + zx$不相等，所以B不正确。
选项C：根据立方和公式，$(x + y)(x^2 - xy + y^2) = x^3 + y^3$，所以C正确。
选项D：根据立方差公式，$(x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3$，所以D正确。
【答案】：B

8. 计算$6m^{6}÷(-2m^{2})^{3}$的结果为 (D)
A.-m
B.-1
C.$\frac {3}{4}$
D.$-\frac {3}{4}$

答案： 【解析】：本题考查整式的除法运算，涉及积的乘方和同底数幂的除法法则。先计算幂的乘方与积的乘方，再进行同底数幂的除法运算。
解：原式$=6m^{6}÷(-8m^{6})$
$=-\frac{6}{8}m^{6 - 6}$
$=-\frac{3}{4}m^{0}$
$=-\frac{3}{4}×1$
$=-\frac{3}{4}$
【答案】：D

9. 若$a^{x}= 3,a^{y}= 2$,则$a^{2x+y}$等于 (D)
A.6
B.7
C.8
D.18

答案： 【解析】：本题考查同底数幂的乘法和幂的乘方运算。根据幂的乘方法则，$a^{2x}=(a^x)^2$，已知$a^x = 3$，则$a^{2x}=3^2 = 9$；再根据同底数幂的乘法法则，$a^{2x + y}=a^{2x} \cdot a^y$，已知$a^y = 2$，所以$a^{2x + y}=9×2 = 18$。
【答案】：D

10. 若$(x^{2}-x+m)(x-8)$中不含x的一次项,则m的值为 (B)
A.8
B.-8
C.0
D.8或-8

答案： 【解析】：本题考查多项式乘法及不含某一项的条件。首先需将$(x^{2}-x+m)(x - 8)$展开，合并同类项后，令一次项系数为$0$，即可求出$m$的值。
展开原式：
$\begin{aligned}&(x^{2}-x+m)(x - 8)\\=&x^{3}-8x^{2}-x^{2}+8x+mx - 8m\\=&x^{3}-9x^{2}+(8 + m)x - 8m\end{aligned}$
因为不含$x$的一次项，所以一次项系数$8 + m = 0$，解得$m=-8$。
【答案】：B

11. 若$2\cdot 8^{n}\cdot 16^{n}= 2^{22}$,则n的值为 (3)
A.3
B.4
C.5
D.6

答案： 【解析】：本题考查幂的运算，需要将等式左边的各项都化为以2为底数的幂，再根据同底数幂相乘，底数不变，指数相加的法则，得到关于n的方程，进而求解n的值。
【答案】：A
解：因为$8^{n}=(2^{3})^{n}=2^{3n}$，$16^{n}=(2^{4})^{n}=2^{4n}$，
所以$2\cdot 8^{n}\cdot 16^{n}=2\cdot 2^{3n}\cdot 2^{4n}$
根据同底数幂相乘，底数不变，指数相加，可得：
$2\cdot 2^{3n}\cdot 2^{4n}=2^{1 + 3n + 4n}=2^{1 + 7n}$
已知$2\cdot 8^{n}\cdot 16^{n}=2^{22}$，所以$2^{1 + 7n}=2^{22}$
则指数相等，即$1 + 7n=22$
解得$7n=21$，$n = 3$

12. 若$(x+a)(x-3)= x^{2}-mx-6$,则m等于 (D)
A.-2
B.2
C.-1
D.1

答案： 【解析】：本题考查多项式乘多项式以及多项式相等的条件。先将左边式子展开：$(x + a)(x - 3) = x^2 - 3x + ax - 3a = x^2 + (a - 3)x - 3a$。因为等式左右两边多项式相等，所以对应项系数相等。即$-3a = -6$，解得$a = 2$；又因为$a - 3 = -m$，将$a = 2$代入可得$2 - 3 = -m$，即$-1 = -m$，所以$m = 1$。
【答案】：D

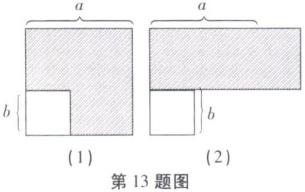
13. 如图所示,从边长为a的大正方形中挖去一个边长是b的小正方形,小明将图(1)中的阴影部分拼成了一个如图(2)所示的矩形,这一过程可以验证 (D)

A.$a^{2}+b^{2}-2ab= (a-b)^{2}$
B.$a^{2}+b^{2}+2ab= (a+b)^{2}$
C.$2a^{2}-3ab+b^{2}= (2a-b)(a-b)$
D.$a^{2}-b^{2}= (a+b)(a-b)$

答案： 【解析】：题目考查的是平方差公式的几何验证。从边长为$a$的大正方形中挖去边长为$b$的小正方形，图（1）阴影部分面积为大正方形面积减去小正方形面积，即$a^2 - b^2$。小明将阴影部分拼成图（2）的矩形，该矩形的长为$a + b$，宽为$a - b$，其面积为$(a + b)(a - b)$。因为阴影部分面积不变，所以$a^2 - b^2=(a + b)(a - b)$，此过程验证了平方差公式。
【答案】：D