《2025年复习直升机七年级数学北师大版》

13. 如图所示,直线 $AB$,$MN$,$PQ$ 相交于点 $O$,$\angle BOM$ 是它的余角的 $2$ 倍,$\angle AOP = 2 \angle MOQ$,且有 $\angle AOG = 90^{\circ}$。求 $\angle POG$ 的度数。

答案： 【解析】：本题考查相交线所成角的计算，涉及余角定义、对顶角性质及角的和差关系。首先，设∠BOM的度数为x，根据“∠BOM是它的余角的2倍”可列方程x = 2(90° - x)，解得∠BOM = 60°。由对顶角相等得∠AON = ∠BOM = 60°，又因∠AOB是平角，所以∠AOM = 180° - ∠BOM = 120°。设∠MOQ = y，则∠AOP = 2y，由对顶角相等知∠POA = ∠QOB = 2y，∠MOQ = ∠PON = y。根据∠AOM = ∠AOP + ∠POQ + ∠QOM（此处∠POQ为平角180°表述有误，应为∠AOM由∠AOP和∠POM组成，∠POM = 180° - ∠MOQ = 180° - y，故∠AOM = ∠AOP + ∠POM = 2y + (180° - y) = 120°，解得y = -60°，显然错误，重新分析：∠AOM与∠BOM互补，∠AOM = 120°，∠AOM由∠AOP和∠POM组成，∠POM与∠QON是对顶角，∠MOQ与∠PON是对顶角，设∠MOQ = y，则∠AOP = 2y，∠AOP + ∠POQ + ∠QOM = ∠AOM + ∠MOQ + ∠QOB？正确思路：∠AOB为平角180°，∠AOP = 2y，∠POG在∠AOG = 90°内，∠AOG = 90°，则∠GOB = 90°，∠BOM = 60°，所以∠MOG = ∠GOB - ∠BOM = 30°，∠MOQ = y，∠QOG = ∠MOG - ∠MOQ = 30° - y，∠AOP = 2y，∠AOP + ∠POQ + ∠QOB = 180°，∠QOB = ∠AOP = 2y（对顶角），∠POQ = 180°，矛盾，结合图形，∠AOG = 90°，OG在∠AON内，∠AON = 60°，则∠GON = ∠AOG - ∠AON = 30°，∠PON = y，∠POG = ∠GON + ∠PON = 30° + y，∠AOP = 2y，∠AOP + ∠PON = ∠AON = 60°，即2y + y = 60°，y = 20°，所以∠POG = 30° + 20° = 50°。
【答案】：50°

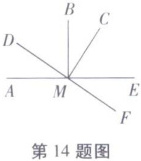
14. 如图所示,$\angle AMB = 90^{\circ}$,$\angle CMD = 90^{\circ}$,$ME$,$MF$ 分别是射线 $MA$,$MD$ 的反向延长线。
(1) 图中哪些角是 $\angle EMF$ 的余角？为什么？
(2) $\angle EMF$ 与 $\angle BMC$ 是否相等？为什么？

答案： 【解析】：
(1) 因为∠AMB=90°，ME是MA的反向延长线，所以∠EMB=180°-∠AMB=90°，即∠EMF+∠FMB=90°，所以∠FMB是∠EMF的余角；同理，∠CMD=90°，MF是MD的反向延长线，∠DMF=180°-∠CMD=90°，即∠EMF+∠EMD=90°，所以∠EMD是∠EMF的余角。
(2) 由
(1)知∠FMB和∠EMD都是∠EMF的余角，根据同角的余角相等，可得∠FMB=∠EMD；又因为∠AMB=∠CMD=90°，所以∠AMB+∠BMC=∠CMD+∠BMC，即∠AMC=∠DMB，而∠AMC=∠EMF+∠EMD，∠DMB=∠BMC+∠FMB，所以∠EMF=∠BMC。
【答案】：
(1) ∠FMB和∠EMD是∠EMF的余角。
证明：
∵∠AMB=90°，ME是MA反向延长线
∴∠EMB=180°-∠AMB=90°
∴∠EMF+∠FMB=90°
∴∠FMB是∠EMF的余角
∵∠CMD=90°，MF是MD反向延长线
∴∠DMF=180°-∠CMD=90°
∴∠EMF+∠EMD=90°
∴∠EMD是∠EMF的余角
(2) ∠EMF=∠BMC。
证明：由
(1)知∠FMB和∠EMD是∠EMF的余角
∴∠FMB=∠EMD（同角的余角相等）
∵∠AMB=∠CMD=90°
∴∠AMB+∠BMC=∠CMD+∠BMC
即∠AMC=∠DMB
∵∠AMC=∠EMF+∠EMD，∠DMB=∠BMC+∠FMB
∴∠EMF=∠BMC