《2025年复习直升机七年级数学北师大版》

例 4 如图所示,在等边三角形 $ A B C $ 中,点 $ P $ 在 $ \triangle A B C $ 内,点 $ Q $ 在 $ \triangle A B C $ 外,且 $ \angle A B P = \angle A C Q $,$ B P = C Q $。
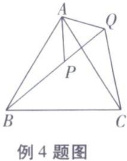
(1) 求证：$ \triangle A B P \cong \triangle A C Q $；
(2) 请判断 $ \triangle A P Q $ 是什么形状的三角形？试说明你的结论。

答案： 【解析】：
(1) 要证△ABP≌△ACQ，已知∠ABP=∠ACQ，BP=CQ。因为△ABC是等边三角形，所以AB=AC，∠BAC=60°。根据SAS（两边及其夹角对应相等的两个三角形全等）可证全等。
(2) 由
(1)中△ABP≌△ACQ可得AP=AQ，∠BAP=∠CAQ。因为∠BAC=∠BAP+∠PAC=60°，所以∠PAQ=∠CAQ+∠PAC=∠BAP+∠PAC=60°，有一个角是60°的等腰三角形是等边三角形，所以△APQ是等边三角形。
【答案】：
(1) 证明：
∵△ABC是等边三角形
∴AB=AC，∠BAC=60°
在△ABP和△ACQ中
∵AB=AC，∠ABP=∠ACQ，BP=CQ
∴△ABP≌△ACQ(SAS)
(2) △APQ是等边三角形
理由如下：
∵△ABP≌△ACQ
∴AP=AQ，∠BAP=∠CAQ
∵∠BAC=∠BAP+∠PAC=60°
∴∠PAQ=∠CAQ+∠PAC=∠BAP+∠PAC=60°
∵AP=AQ，∠PAQ=60°
∴△APQ是等边三角形

例 5 如图所示,在 $ \triangle A B C $ 中,$ A B = A C = 2 $,$ \angle B = \angle C = 40 ^ { \circ } $,点 $ D $ 在线段 $ B C $ 上运动不与 $ B $,$ C $ 重合,连接 $ A D $,作 $ \angle A D E = 40 ^ { \circ } $,$ D E $ 交线段 $ A C $ 于 $ E $。
(1) 当 $ \angle B D A = 115 ^ { \circ } $ 时,$ \angle E D C = $25$ ^ { \circ } $,$ \angle D E C = $115$ ^ { \circ } $；点 $ D $ 从 $ B $ 向 $ C $ 运动时,$ \angle B D A $ 逐渐变小(填“大”或“小”)。
(2) 当 $ D C $ 等于多少时,$ \triangle A B D \cong \triangle D C E $,请说明理由。
(3) 在点 $ D $ 的运动过程中,$ \triangle A D E $ 的形状可以是等腰三角形吗？若可以,请直接写出 $ \angle B D A $ 的度数；若不可以,请说明理由。

答案： 【解析】：
(1)在△ABC中，已知AB=AC=2，∠B=∠C=40°，点D在线段BC上运动，∠ADE=40°，DE交AC于E。当∠BDA=115°时，在△ABD中，根据三角形内角和为180°，可求出∠BAD=180°-∠B-∠BDA=180°-40°-115°=25°。因为∠BAC=180°-∠B-∠C=100°，所以∠DAC=∠BAC-∠BAD=100°-25°=75°。在△ADE中，∠ADE=40°，∠DAC=75°，则∠AED=180°-∠ADE-∠DAC=180°-40°-75°=65°，所以∠DEC=180°-∠AED=180°-65°=115°。又因为∠ADC=180°-∠BDA=180°-115°=65°，∠ADE=40°，所以∠EDC=∠ADC-∠ADE=65°-40°=25°。当点D从B向C运动时，∠BDA逐渐变小。
(2)要使△ABD≌△DCE，已知∠B=∠C=40°，∠ADB+∠ADE+∠EDC=180°，∠ADE=40°，所以∠ADB+∠EDC=140°，又因为∠DEC+∠EDC+∠C=180°，所以∠DEC+∠EDC=140°，故∠ADB=∠DEC。若△ABD≌△DCE，根据AAS或ASA，当AB=DC时，AB=2，所以DC=2。
(3)△ADE为等腰三角形有三种情况：①AD=AE时，∠ADE=∠AED=40°，则∠DAE=100°，但∠BAC=100°，此时D与B重合，不符合题意；②AD=DE时，∠DAE=∠AED=(180°-40°)/2=70°，则∠BAD=∠BAC-∠DAE=30°，∠BDA=180°-∠B-∠BAD=110°；③AE=DE时，∠DAE=∠ADE=40°，则∠BAD=∠BAC-∠DAE=60°，∠BDA=180°-∠B-∠BAD=80°。所以∠BDA的度数为110°或80°。
【答案】：
(1)25；115；小
(2)DC=2。理由如下：
证明：
∵AB=AC=2，∠B=∠C=40°
∵∠ADB+∠ADE+∠EDC=180°，∠ADE=40°
∴∠ADB+∠EDC=140°
∵∠DEC+∠EDC+∠C=180°
∴∠DEC+∠EDC=140°
∴∠ADB=∠DEC
在△ABD和△DCE中，∠B=∠C，∠ADB=∠DEC，AB=DC=2
∴△ABD≌△DCE(AAS)
(3)可以，∠BDA的度数为80°或110°