《2025年复习直升机七年级数学北师大版》

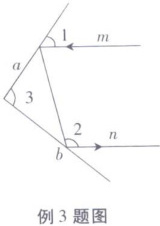
例3 平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图所示,一束光线$m先射到平面镜a$上,被平面镜$a反射到平面镜b$上,又被平面镜$b反射出光线n$。
(1)若$m// n$,且$∠1= 50^{\circ }$,则$∠2= $40$^{\circ }$,$∠3= $90$^{\circ }$；
(2)若$m// n$,且$∠1= 40^{\circ }$,则$∠3= $90$^{\circ }$；
(3)根据(1)、(2)猜想：当两平面镜$a$,$b的夹角∠3$是多少度时,总有$m// n$？试证明你的猜想。

答案： 【解析】：（1）根据平面镜反射规律，射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等。已知∠1=50°，所以光线m与平面镜a的夹角为∠1=50°，则反射光线与平面镜a的夹角也为50°，那么反射光线与光线m的夹角为180°-50°-50°=80°，即反射光线与平面镜a的夹角的余角为90°-50°=40°，所以反射光线与平面镜a的法线夹角为40°，则反射光线与平面镜a的夹角为50°，所以反射光线与平面镜a形成的角中，另一个角为180°-90°-40°=50°（此处可能表述稍显复杂，换一种思路：设光线m与平面镜a的交点为O，法线为ON，则∠mON=90°-∠1=90°-50°=40°，根据反射定律，反射角等于入射角，所以反射光线与法线ON的夹角也为40°，则反射光线与平面镜a的夹角为∠1=50°，即反射光线与平面镜a的夹角为50°，所以反射光线与平面镜a形成的角为50°，那么这条反射光线与平面镜b相交，设交点为P，此时这条反射光线是入射到平面镜b上的光线，设它与平面镜b的夹角为∠4，则根据反射规律，反射出的光线n与平面镜b的夹角也为∠4，即∠2=∠4。
因为m//n，所以过点O和点P作辅助线，利用平行线的性质和三角形内角和定理。光线m与反射光线（从a到b的光线）的夹角为180°-2∠1=180°-2×50°=80°，光线n与反射光线（从a到b的光线）的夹角为180°-2∠2=180°-2∠4。因为m//n，所以这两个夹角之和等于平面镜a和b的夹角∠3的补角？或者在由O、P以及两平面镜交点（设为Q）组成的三角形中，∠OQP=∠3，∠O=180°-2∠1=80°，∠P=180°-2∠2=180°-2∠4，因为m//n，所以∠O + ∠P + ∠3=180°（两直线平行，同旁内角互补的推广？或者利用内错角相等）。因为m//n，所以光线m与光线n的内错角相等，即光线m与反射光线的夹角加上反射光线与光线n的夹角等于180°-∠3？或者在三角形OPQ中，∠O=180°-2∠1=80°，∠P=180°-2∠2，∠3是三角形的一个内角，所以∠O + ∠P + ∠3=180°，即80° + (180°-2∠2) + ∠3=180°，又因为m//n，所以∠1 + ∠2 + ∠3=90° + 90°=180°？（因为光线m与平面镜a夹角∠1，所以光线m与a的法线夹角为90°-∠1，反射光线与a的法线夹角也为90°-∠1，所以光线m与反射光线的夹角为2(90°-∠1)=180°-2∠1，同理光线n与反射光线的夹角为2(90°-∠2)=180°-2∠2，因为m//n，所以这两个夹角之和等于180°（同旁内角互补），即(180°-2∠1)+(180°-2∠2)=180°，化简得360°-2(∠1+∠2)=180°，所以2(∠1+∠2)=180°，∠1+∠2=90°，已知∠1=50°，所以∠2=40°。
在三角形OPQ中，∠3 + ∠(180°-∠1-∠4)=180°？因为∠1=50°，∠4=∠2=40°，所以∠3=∠1 + ∠2=50°+40°=90°。所以∠2=40°，∠3=90°。
（2）当∠1=40°时，同理，由（1）中得出的∠1+∠2=90°，所以∠2=90°-∠1=50°，再根据三角形内角和或前面的规律，∠3=∠1+∠2=40°+50°=90°。
（3）猜想∠3=90°时，总有m//n。
证明：设光线m与平面镜a的夹角为∠1，则根据反射定律，反射光线与平面镜a的夹角也为∠1，所以这条反射光线（入射到平面镜b上）与平面镜a的夹角为∠1，那么它与平面镜b的夹角设为∠4，因为两平面镜夹角为∠3，在两平面镜的交点处，根据三角形外角定理，∠1 + ∠4=∠3。当∠3=90°时，∠1 + ∠4=90°。根据反射定律，光线n与平面镜b的夹角等于∠4，即∠2=∠4，所以∠1 + ∠2=90°。此时光线m与反射光线（a到b）的夹角为180°-2∠1，光线n与反射光线（a到b）的夹角为180°-2∠2，两者之和为(180°-2∠1)+(180°-2∠2)=360°-2(∠1+∠2)=360°-2×90°=180°，所以光线m与光线n平行（同旁内角互补，两直线平行）。
【答案】：
(1)50,90；
(2)90；
(3)90°

例4 已知：如图(1)、(2)所示,解答下面各题：

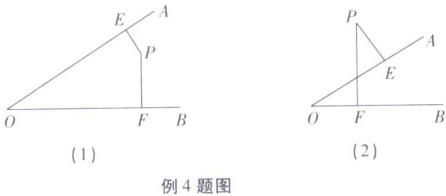
(1)图(1)中,$∠AOB= 55^{\circ }$,点$P在∠AOB$内部,过点$P作PE⊥OA$,$PF⊥OB$,垂足分别为$E$,$F$,求$∠EPF$的度数。
(2)图(2)中,点$P在∠AOB$外部,过点$P作PE⊥OA$,$PF⊥OB$,垂足分别为$E$,$F$,那么$∠P与∠O$有什么关系？为什么？
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系？
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系？(请画图说明结果,不需要过程)

答案： 【解析】：
(1)因为PE⊥OA，PF⊥OB，所以∠OEP=∠OFP=90°。在四边形OEPF中，内角和为360°，∠AOB=55°，所以∠EPF=360°-∠OEP-∠OFP-∠AOB=360°-90°-90°-55°=125°。
(2)因为PE⊥OA，PF⊥OB，所以∠OEP=∠OFP=90°。设OA与PF相交于点C，在△OFC和△PEC中，∠OCF=∠PCE（对顶角相等），所以∠P=∠O（等角的余角相等）。
(3)由
(1)中∠EPF=125°与∠AOB=55°互补，
(2)中∠P=∠O，可得如果一个角的两边分别垂直于另一个角的两边，则这两个角相等或互补。
(4)如果一个角的两边分别平行于另一个角的两边，这两个角相等或互补（画图略）。
【答案】：
(1)125°；
(2)相等；
(3)相等或互补；
(4)相等或互补