《2025年春雨教育小学数学应用题解题高手五年级上册苏教版》

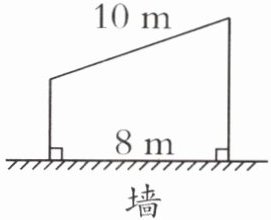
典型例题 五(1)班的同学们用 56 米长的篱笆靠墙围了一块地(如右图),这块地的面积是多少平方米?

 

答案： 56 - 10 = 46(米)
46×8÷2 = 184(平方米)
答:这块地的面积是184平方米。

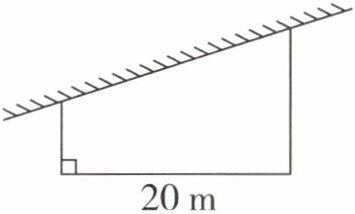
1. 如右下图,刘爷爷用篱笆围了一块靠墙的梯形菜地,它的面积是 170 平方米,这排篱笆长多少米?

答案： 170×2÷20+20=37(米)
提示 观察题图,根据上底+下底=梯形面积×2÷高,据此代入数据可以求出该梯形上底加下底的和,再加上梯形的高,即为篱笆的长度。

2. 李叔叔要建造一个花圃,花圃的一边靠墙,围花圃的篱笆长 40 m,他设计了两种方案。(如右下图,单位:m)
(1)这两种方案围成的花圃,面积相差多少平方米?

(2)按面积大的方案建成花圃,在花圃中种上玫瑰,如果每平方米可以种 20 株,每株玫瑰从种植到成品需要 4 元,那么种这些玫瑰一共需要多少元?

答案：
(1)①:40-10=30(米)
30×10÷2=150(平方米)
②:40-10=30(米)
30×8÷2=120(平方米)
150-120=30(平方米)
(2)150×20×4=12000(元)
提示
(1)首先用周长40米分别减去10米求出两个梯形的上底与下底的和,然后根据梯形的面积公式求出两个梯形的面积,最后求出两个梯形的面积差。
(2)用梯形的面积乘20求出种玫瑰的数量,然后再乘4就是需要的钱数。