《2025年53全优卷六年级数学上册苏教版》

8. 如图,用棱长2厘米的小正方体拼成一个长方体,按照这样的拼法,第n个长方体的表面积是( )平方厘米。(用含有字母的式子表示)

答案： 第1个长方体：长4厘米，宽2厘米，高2厘米，表面积为$(4×2 + 4×2 + 2×2)×2 = 40$平方厘米；
第2个长方体：长6厘米，宽2厘米，高2厘米，表面积为$(6×2 + 6×2 + 2×2)×2 = 56$平方厘米；
第3个长方体：长8厘米，宽2厘米，高2厘米，表面积为$(8×2 + 8×2 + 2×2)×2 = 72$平方厘米；
观察可得，第n个长方体长为$2(n + 1)$厘米，宽和高均为2厘米，表面积为$[2(n + 1)×2 + 2(n + 1)×2 + 2×2]×2 = 16n + 24$平方厘米。
16n + 24

1. 把自己的一只拳头握紧,浸没在装满水的脸盆中,溢出水的体积有可能( )。

A.大于1毫升,小于10毫升
B.大于50毫升,小于1升
C.大于1升,小于1立方米
D.大于1.2升,小于1.8升

答案： 解析：本题考查的是对生活中常见物体体积的估测以及单位换算的知识点。需要理解毫升、升、立方米等体积单位的大小，并能根据生活经验估测拳头的体积。
选项A，考虑毫升是较小的体积单位，1毫升相当于一个非常小的体积，而拳头的体积明显大于这个数值，所以A选项不合理。
选项B，50毫升到1升之间的体积范围符合一个拳头的体积估测。因为1升等于1000毫升，也等于0.001立方米，这是一个比较合理的范围。
选项C，1立方米是一个相对较大的体积，远大于一个拳头的体积，所以C选项不合理。
选项D，1.2升到1.8升的体积范围明显大于一个拳头的体积，因此D选项也不合理。
答案：B。

2. 如图,正方体水塔上有一张高1米的附着式警示牌,试估计该水塔的体积是( )。


A.64立方米
B.27立方米
C.16立方米
D.8立方米

答案： 观察图中正方体水塔与高1米的警示牌高度对比，估计正方体水塔棱长约为3米。
正方体体积=棱长×棱长×棱长，即$3×3×3 = 27$（立方米）。
答案：B

3. 下面正方体的展开图是( )。

答案： C

4. 将右图所示的大长方体(单位:厘米),切成两个完全相同的小长方体,它们的表面积之和比原来最多增加( )平方厘米。


A.80
B.96
C.120
D.160

答案： 原长方体长10厘米、宽8厘米、高6厘米。
切成两个完全相同的小长方体，表面积增加两个切面面积。
情况1：平行于长×宽面切，增加面积：10×8×2=160平方厘米。
情况2：平行于长×高面切，增加面积：10×6×2=120平方厘米。
情况3：平行于宽×高面切，增加面积：8×6×2=96平方厘米。
160＞120＞96，最多增加160平方厘米。
D

5. 一个长方体的长、宽、高分别是a米、b米、h米,如果高缩短2米,长、宽不变,那么新的长方体体积比原来小( )立方米。

A.2ab
B.2abh
C.ab(h+2)
D.4a+4b

答案： 解析：
首先，我们需要知道长方体的体积计算公式：$V = 长 × 宽 × 高$。
原长方体的体积为：$V_1 = a × b × h = abh$ 立方米。
当长方体的高缩短2米后，新的高度为 $h-2$ 米，所以新的体积为：
$V_2 = a × b × (h - 2) = ab(h - 2) = abh - 2ab$ 立方米。
新旧体积的差值为：
$V_1 - V_2 = abh - (abh - 2ab) = 2ab$ 立方米。
所以，新的长方体体积比原来小了 $2ab$ 立方米。
答案：A

6. 一个密封的长方体玻璃容器中装了120升的水,将容器按如图所示的三种方式放置后,分别测量出水的高度。该长方体容器的表面积是( )平方分米。(玻璃的厚度忽略不计)


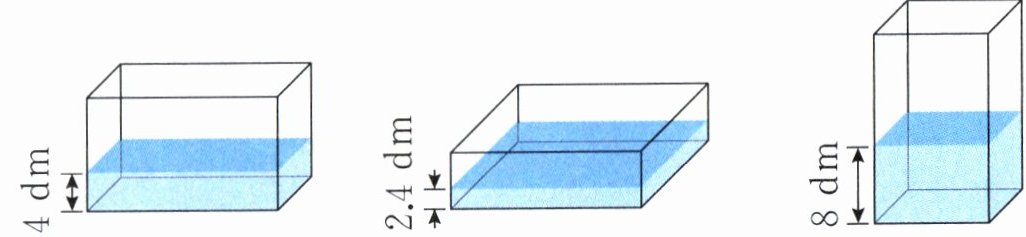
A.190
B.280
C.322
D.450

答案： 120升=120立方分米
设长方体长、宽、高分别为a、b、c（分米）。
由图1：ab×4=120→ab=30
由图2：ac×2.4=120→ac=50
由图3：bc×8=120→bc=15
表面积=2(ab+ac+bc)=2×(30+50+15)=190
A

7. 小明有6根8厘米和9根10厘米的小棒,用其中的12根搭了一个长方体,这个长方体的棱长总和是( )厘米。

A.6×8+9×10= 138
B.(6+9+12)×4= 108
C.6×8+6×10= 108
D.4×8+8×10= 112

答案： 长方体有12条棱，分为3组，每组4条棱长度相等。
情况1：选择8厘米、8厘米、10厘米的小棒各4根。需要8厘米小棒：4×2=8根，小明只有6根8厘米小棒，不符合。
情况2：选择8厘米、10厘米、10厘米的小棒各4根。需要8厘米小棒4根，10厘米小棒：4×2=8根。6≥4，9≥8，符合条件。
棱长总和：4×8 + 8×10 = 32 + 80 = 112厘米。
D